Lecture 13: Poisson Regression
4/4/23
📋 Lecture Outline
- Gaussian v Poisson
- Assumptions
- Gaussian outcomes
- Poisson outcomes
- Offset
- Dispersion
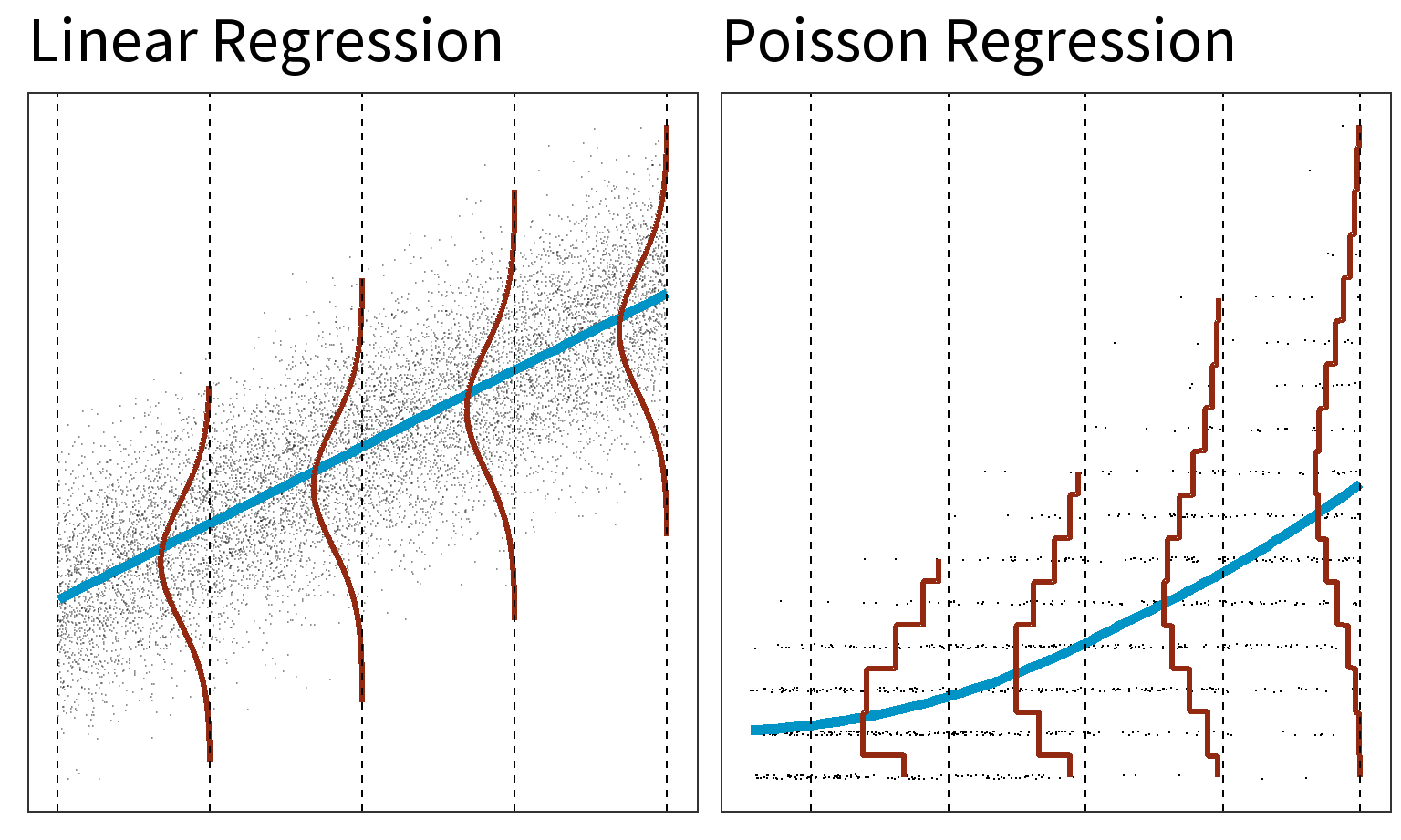
Gaussian v Poisson
Assumptions
Gaussian
- Linearity
- Homoscedasticity
- Normality
- Independence
Poisson
- Log-linearity
- Mean = Variance
- Poisson
- Independence
Gaussian response
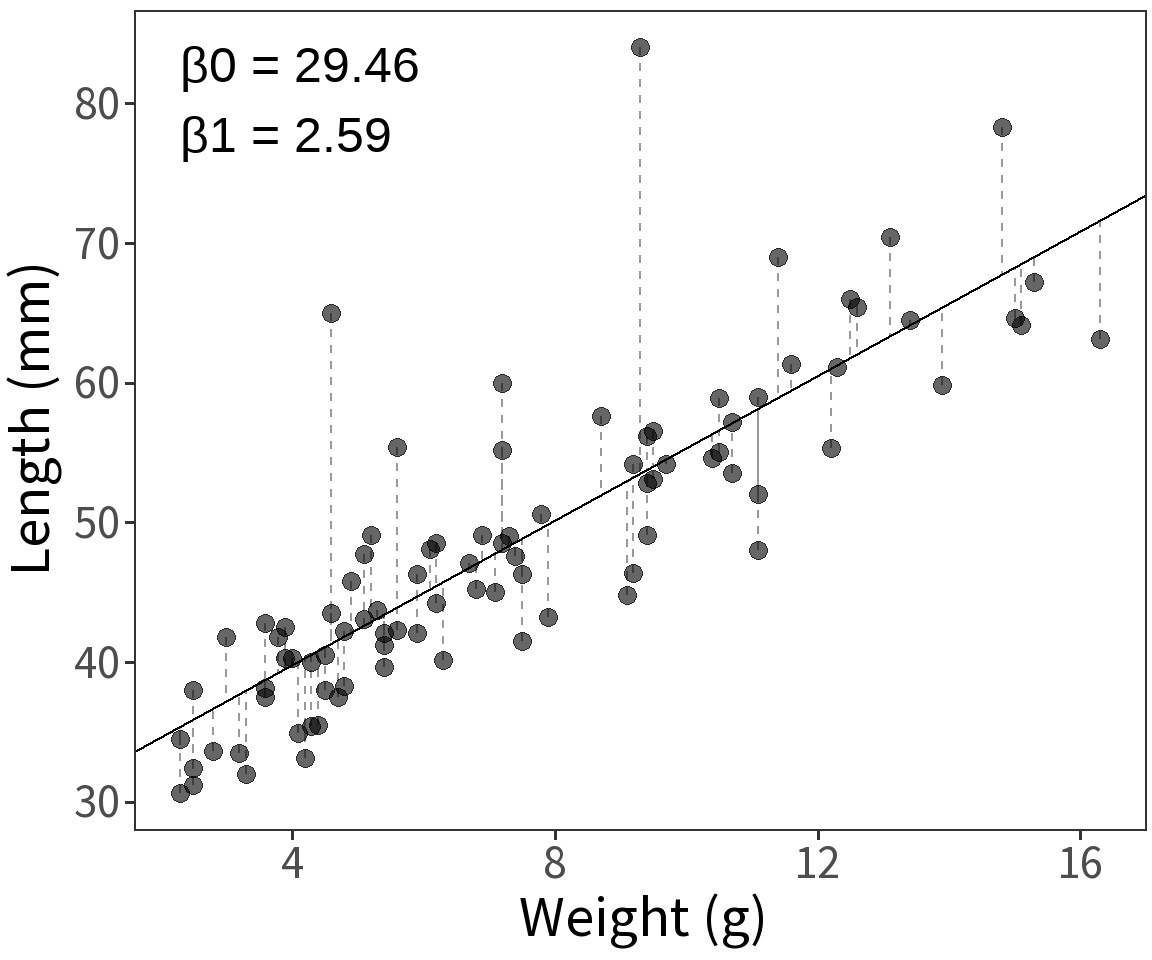
Assume length is Gaussian with
\(Var(\epsilon) = \sigma^2\)
\(E(Y) = \mu = \beta X\)
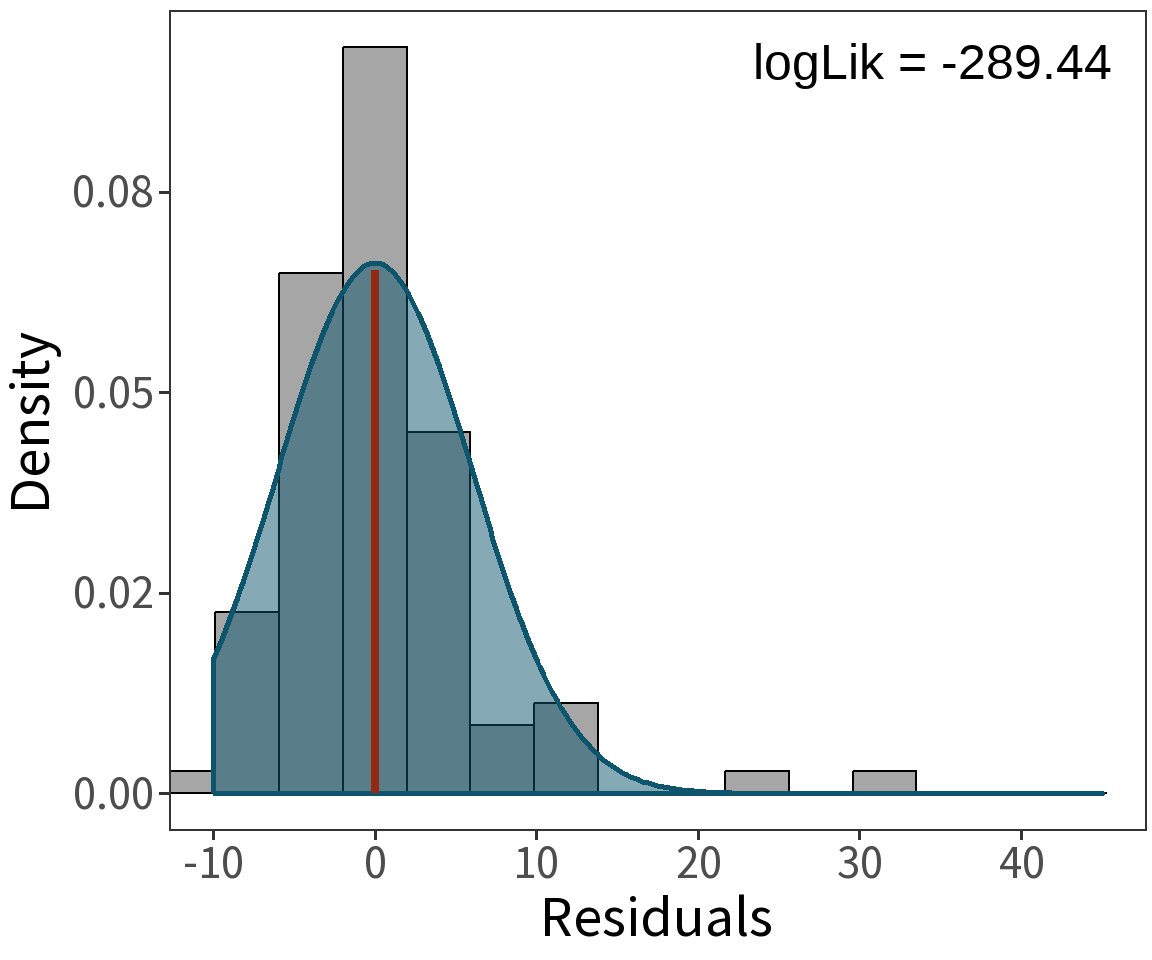
Question What is the probability that we observe these data given a model with parameters \(\beta\) and \(\sigma^2\)?
Poisson GLM
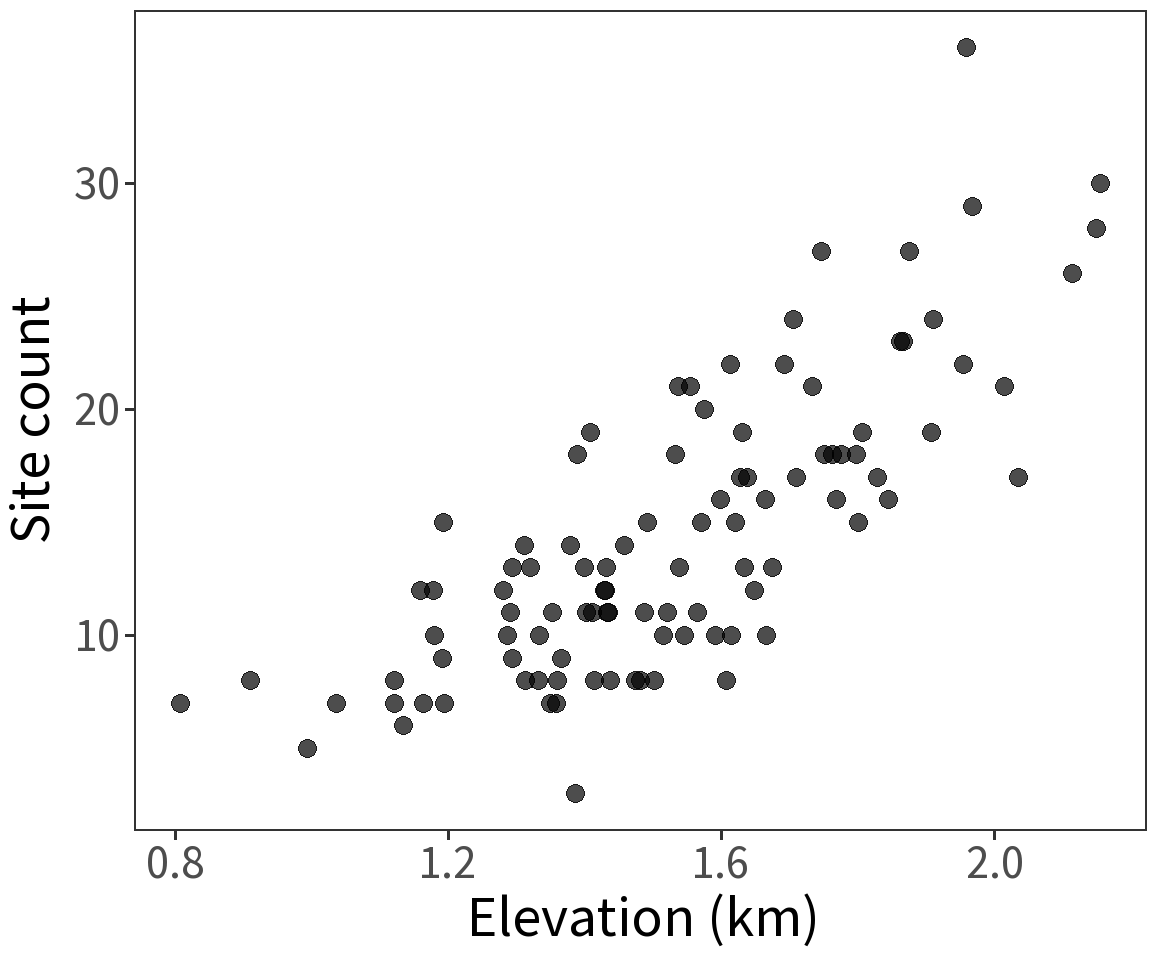
Counts arise from a Poisson process with expectation \(E(Y) = \lambda\) and
\[log\,\lambda = \beta X\]
By taking the log, this constrains the expected count to be greater than zero.
Estimated coefficients:
\(\beta_0 = 0.7074\)
\(\beta_1 = 1.2442\)
⚠️ Coefficients are on the log scale! To get counts, need the exponent.
\(\beta_0 = exp(0.7074) = 2.0286\)
\(\beta_1 = exp(1.2442) = 3.4701\)
For a one unit increase in elevation, the count of sites increases by 3.4701.
A count relative to what?
Survey blocks? Need to account for area in our sampling strategy!
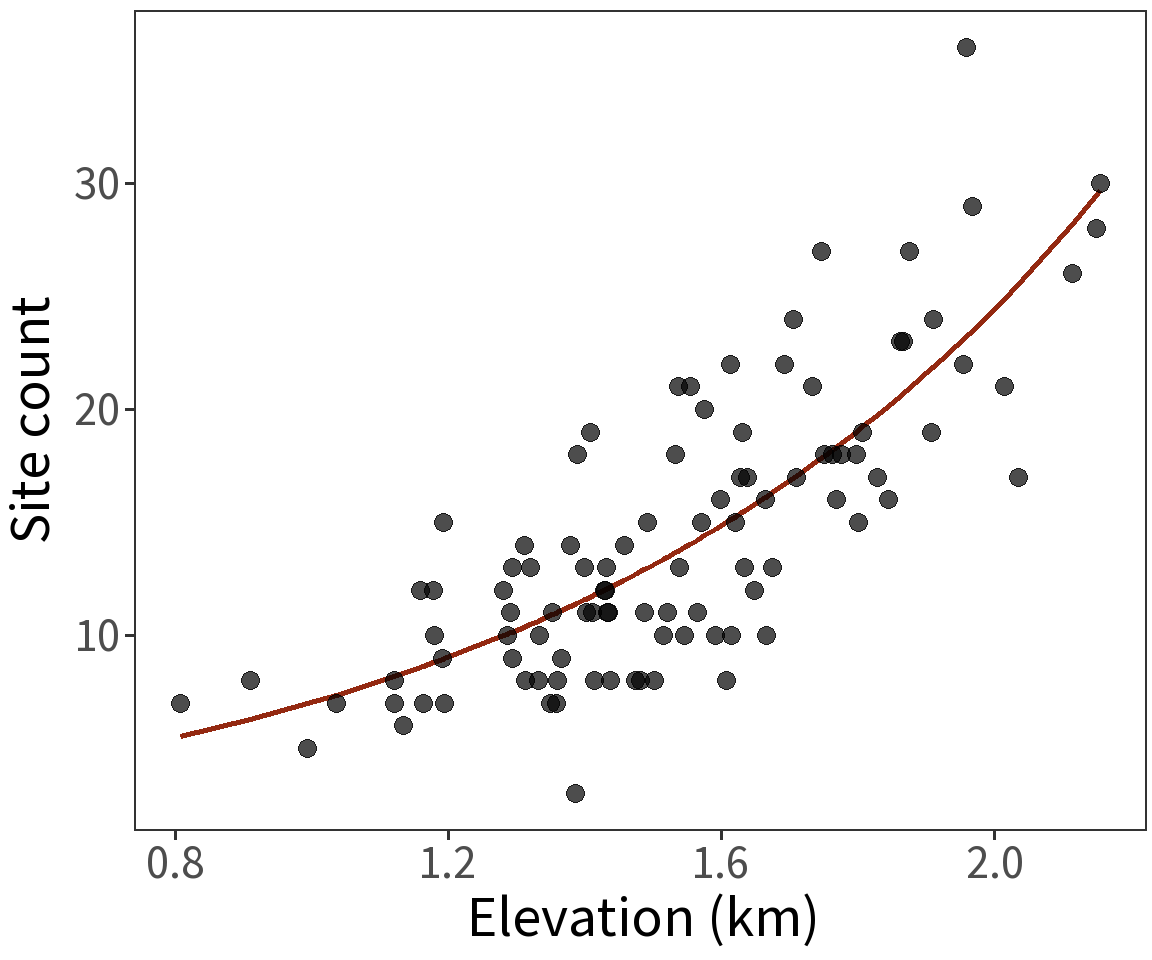
Offset
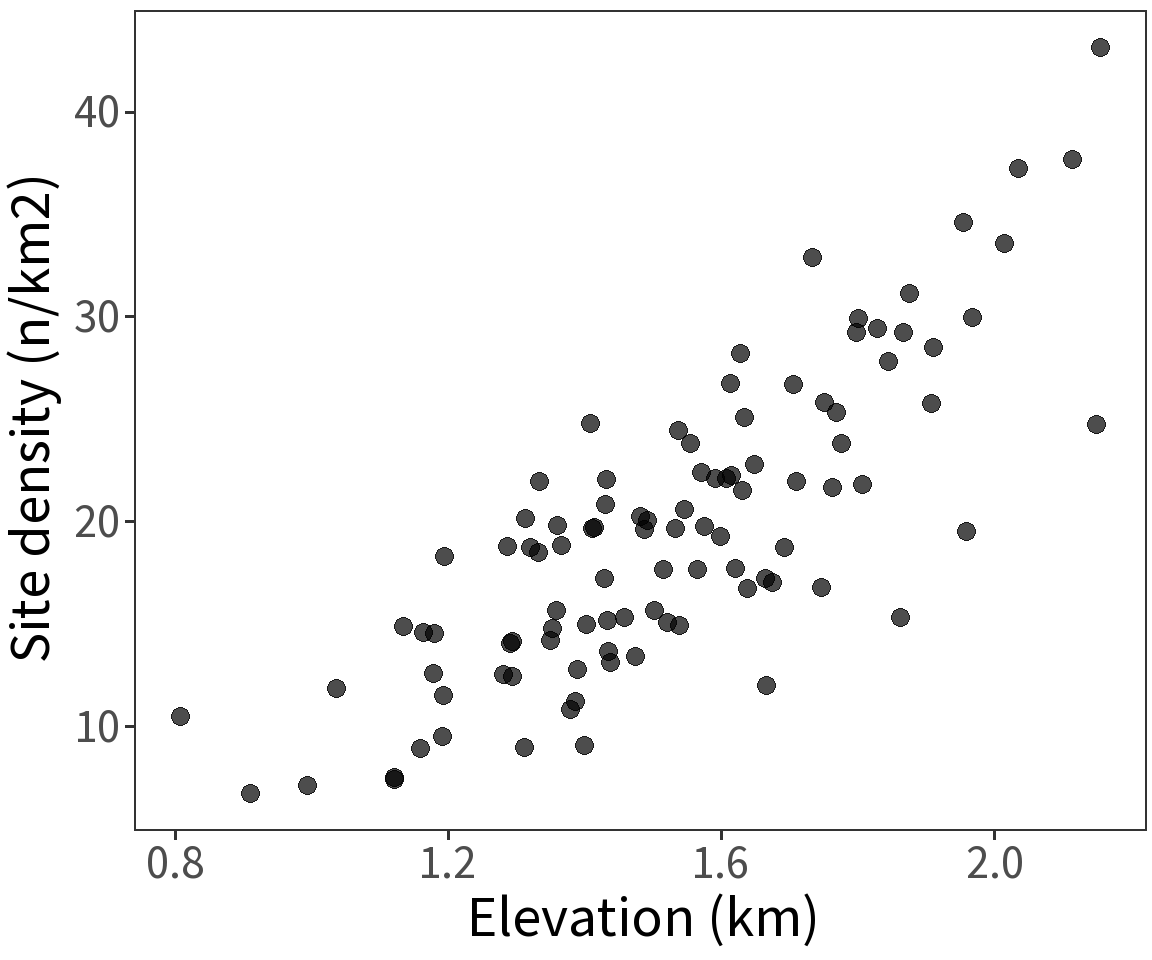
Model the density
\[log\;(\lambda_i/area_i) = \beta X\] Equivalent to
\[log\;(\lambda_i) = \beta X + log\;(area_i)\]
Still linear! Still modeling counts!
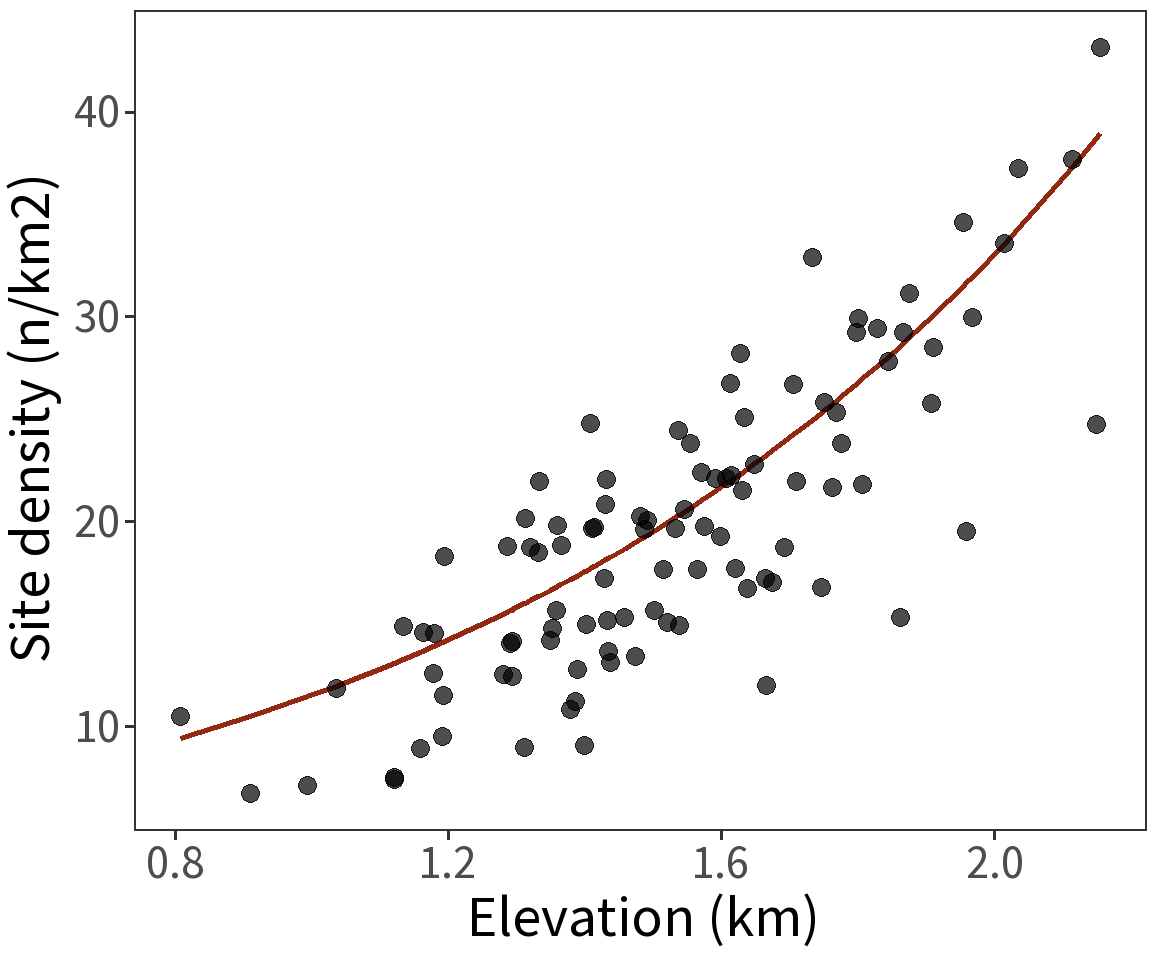
Estimated coefficients:
\(\beta_0 = 1.3899\)
\(\beta_1 = 1.0537\)
For these, the log Likelihood is
\(\mathcal{l} = -444.0432\)
Over-dispersion
- For exponential family of distributions, variance is a function of the mean:
\[Var(\epsilon) = \phi \mu\]
where \(\phi\) is a scaling parameter, assumed to be equal to 1, meaning the variance is assumed to be equal to the mean.
- When \(\phi > 1\), this is called over-dispersion. When \(\phi < 1\), it’s under-dispersion.
Check for over-dispersion
Rule of thumb: compare model’s residual deviance to its degrees of freedom. Values greater than one indicate over-dispersion.
For our site count model, that’s
\(D = 288.1438\)
\(df = 98\)
\(D/df = 2.9402\)
Can also test for dispersion using a simple linear model where
\[Var(\epsilon) = \mu + \alpha \mu\]
If variance is equal to the mean, then \(\alpha = 0\).
| estimate | statistic | null | p.value |
|---|---|---|---|
| 1.8372 | 5.1420 | 0.0000 | 0.0000 |
Accounting for dispersion
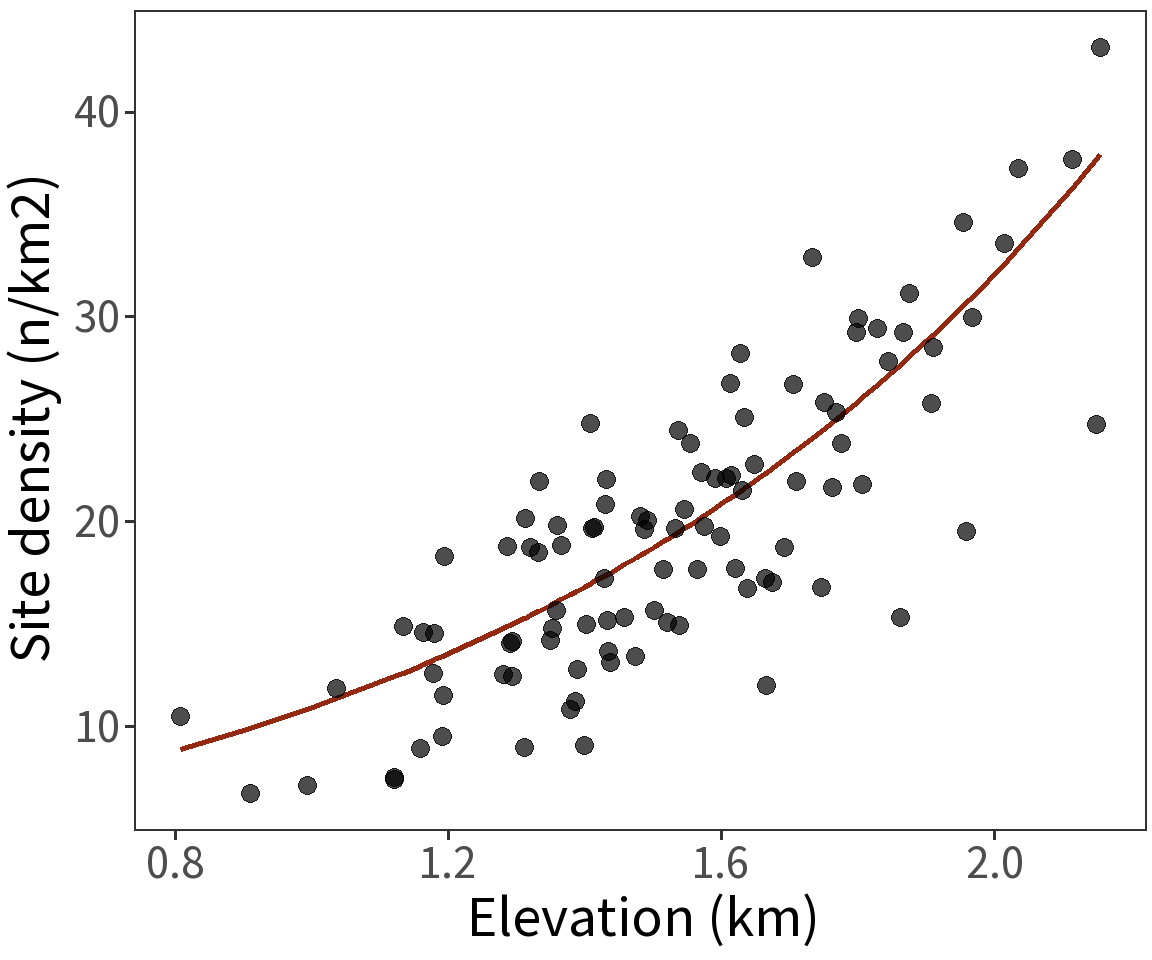
Two strategies:
- quasi-Poisson
- negative binomial
⚠️ Trade-offs! QP doesn’t use MLE. NB can’t be fit with stats::glm().
(1) |
||||
|---|---|---|---|---|
| Est. | S.E. | t | p | |
| (Intercept) | 1.314 | 0.120 | 10.986 | <0.001 |
| elevation | 1.077 | 0.076 | 14.197 | <0.001 |