Lecture 12: Logistic Regression
3/28/23
📋 Lecture Outline
- General Linear Model
- Generalized Linear Model
- Distribution function
- Linear predictor
- Link function
- Gaussian outcomes
- Bernoulli outcomes
- Proportional outcomes
- Deviance
- Information Criteria
- ANOVE aka Likelihood Ratio Test
General Linear Models
\[y = E(Y) + \epsilon\] \[E(Y) = \mu = \beta X\]
- \(E(Y)\) is the expected value (equal to the conditional mean, \(\mu\))
- \(\beta X\) is the linear predictor
- Error is normal, \(\epsilon \sim N(0, \sigma^2)\)
Generalized Linear Models
\[y = E(Y) + \epsilon\] \[E(Y) = g(\mu) = \beta X\]
- \(g\) is the link function, makes the relationship linear
- \(\beta X\) is the linear predictor
- Error is exponential, \(\epsilon \sim Exponential\)
Generalized Linear Models
- A family of distributions:
- Normal - continuous and unbounded
- Gamma - continuous and non-negative
- Binomial - binary (yes/no) or proportional (0-1)
- Poisson - count data
- Describes the distribution of the response
- Two parameters: mean and variance
- Variance is a function of the mean:
\[Var(\epsilon) = \phi \mu\]
where \(\phi\) is a scaling parameter, assumed to be equal to 1, meaning the variance is assumed to be equal to the mean.
- Incorporates information about independent variables
- Combination of \(x\) variables and associated coefficients
\[\beta X = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_n x_n\]
- Commonly denoted with Greek letter “eta”, as in \(\eta = \beta X\)
- \(g()\) modifies relationship between predictors and expected value.
- Makes this relationship linear
| Distribution | Name | Link | Mean |
|---|---|---|---|
| Normal | Identity | \(\beta X = \mu\) | \(\mu = \beta X\) |
| Gamma | Inverse | \(\beta X = \mu^{-1}\) | \(\mu = (\beta X)^{-1}\) |
| Poisson | Log | \(\beta X = ln\,(\mu)\) | \(\mu = exp\, (\beta X)\) |
| Binomial | Logit | \(\beta X = ln\, \left(\frac{\mu}{1-\mu}\right)\) | \(\mu = \frac{1}{1+exp\, (-\beta X)}\) |
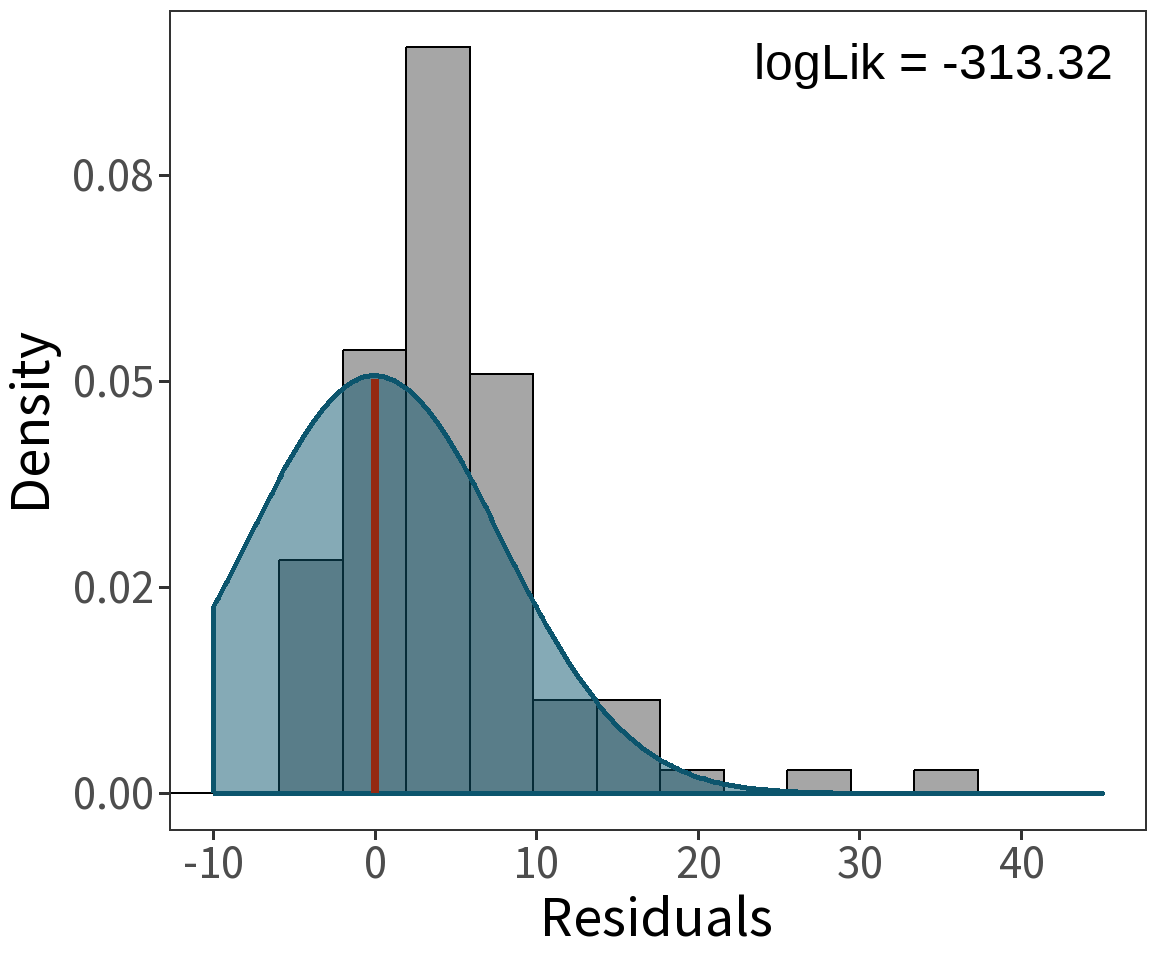
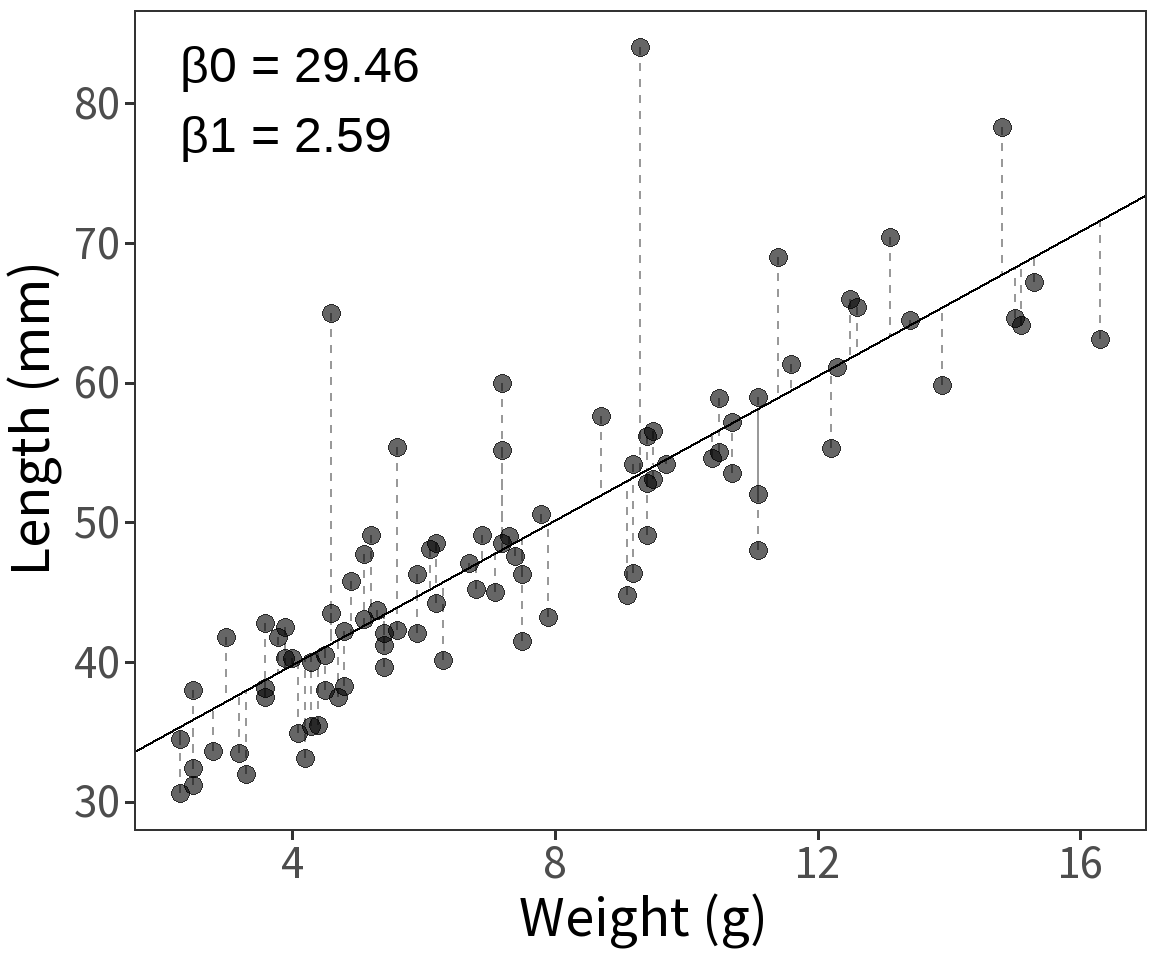
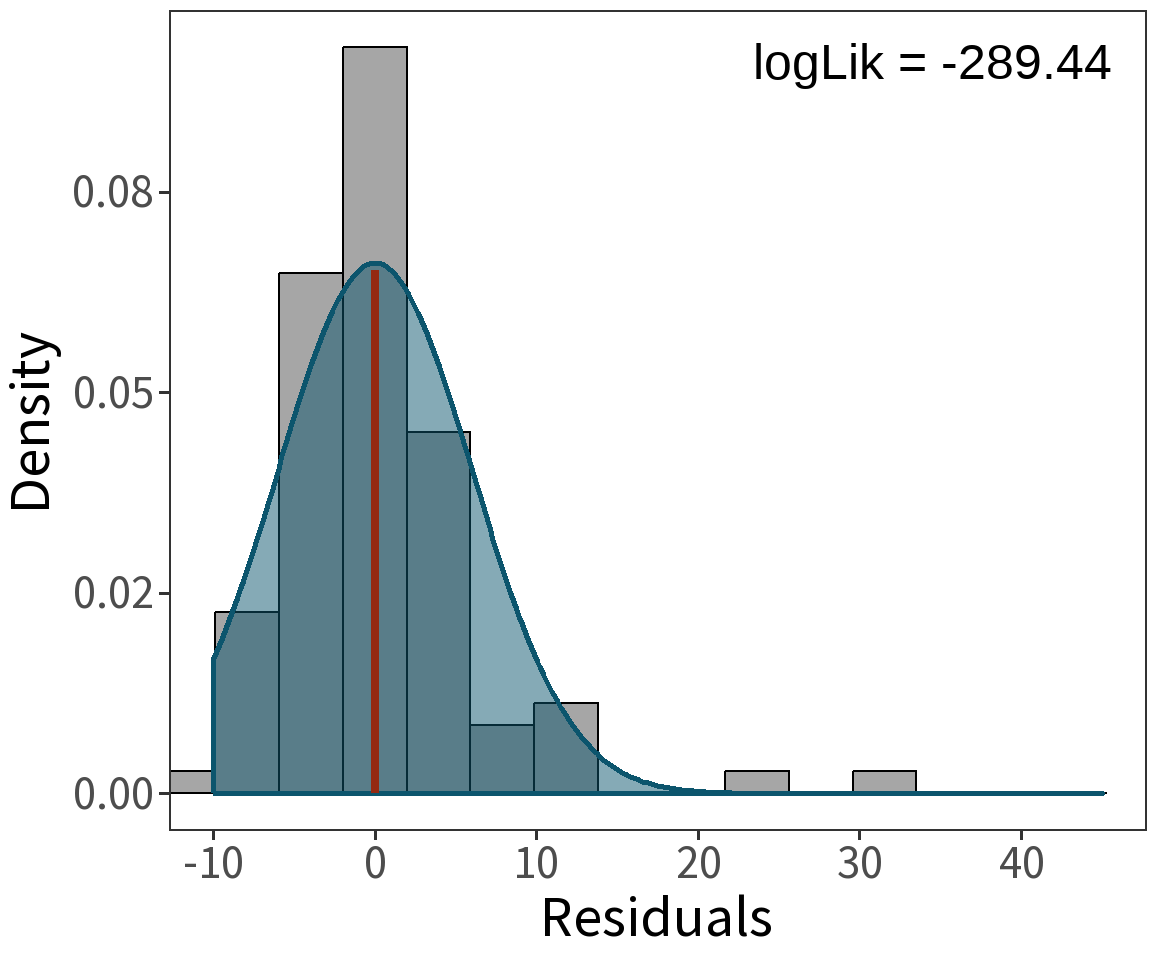
Gaussian response
Assume length is Gaussian with
\(Var(\epsilon) = \sigma^2\)
\(E(Y) = \mu = \beta X\)
Question What is the probability that we observe these data given a model with parameters \(\beta\) and \(\sigma^2\)?
Log Odds
Location of residential features at the Snodgrass sites
| Inside wall | Outside wall | Total | |
|---|---|---|---|
| Count | 38 | 53 | 91 |
| Probability | 0.42 = \(\frac{38}{91}\) | 0.58 = \(\frac{53}{91}\) | 1 |
| Odds | 0.72 = \(\frac{0.42}{0.58}\) | 1.40 = \(\frac{0.58}{0.42}\) | |
| Log Odds | -0.33 = log(0.72) | 0.33 = log(1.40) |
Why Log Odds?
Because the distribution of odds can be highly skewed, and taking the log normalizes it (makes it more symmetric).
Bernoulli response
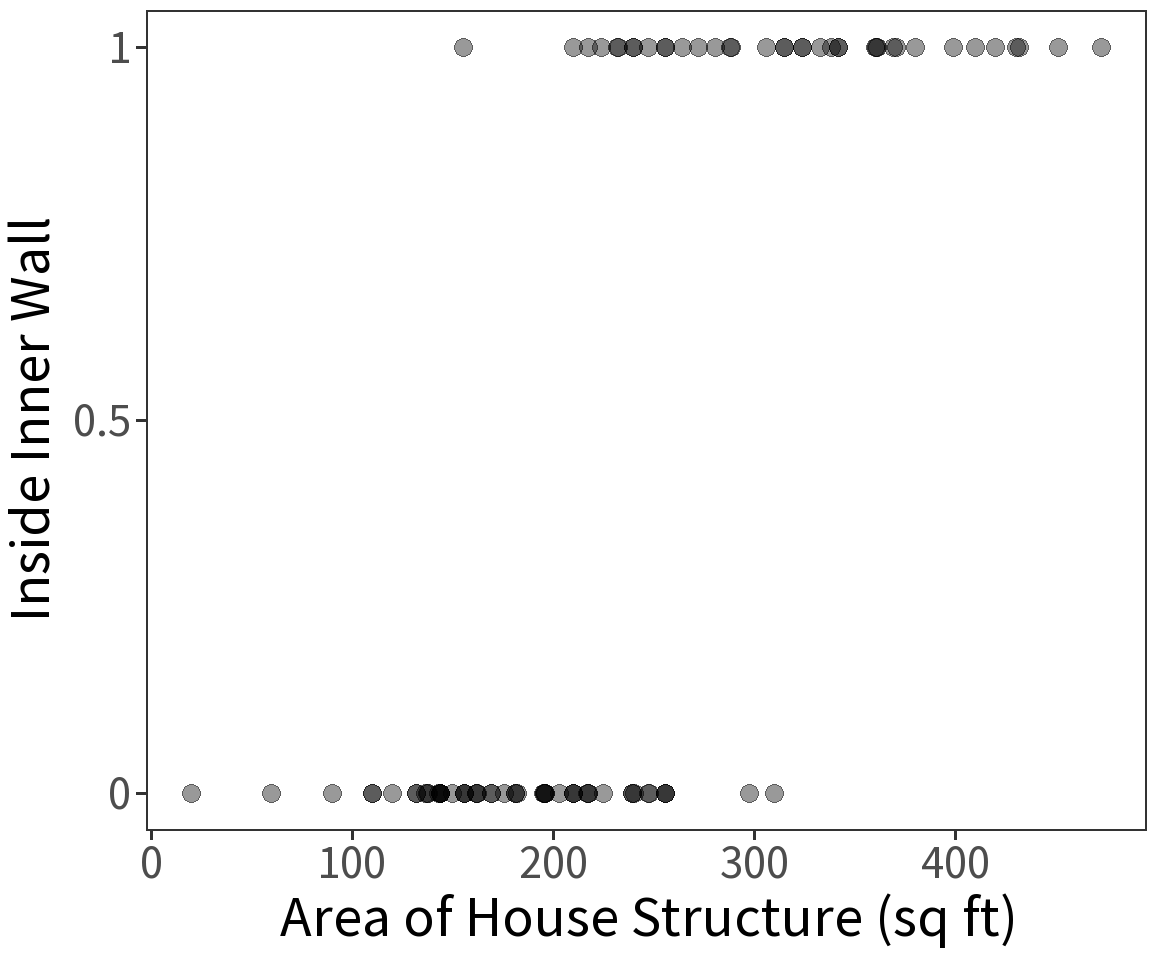
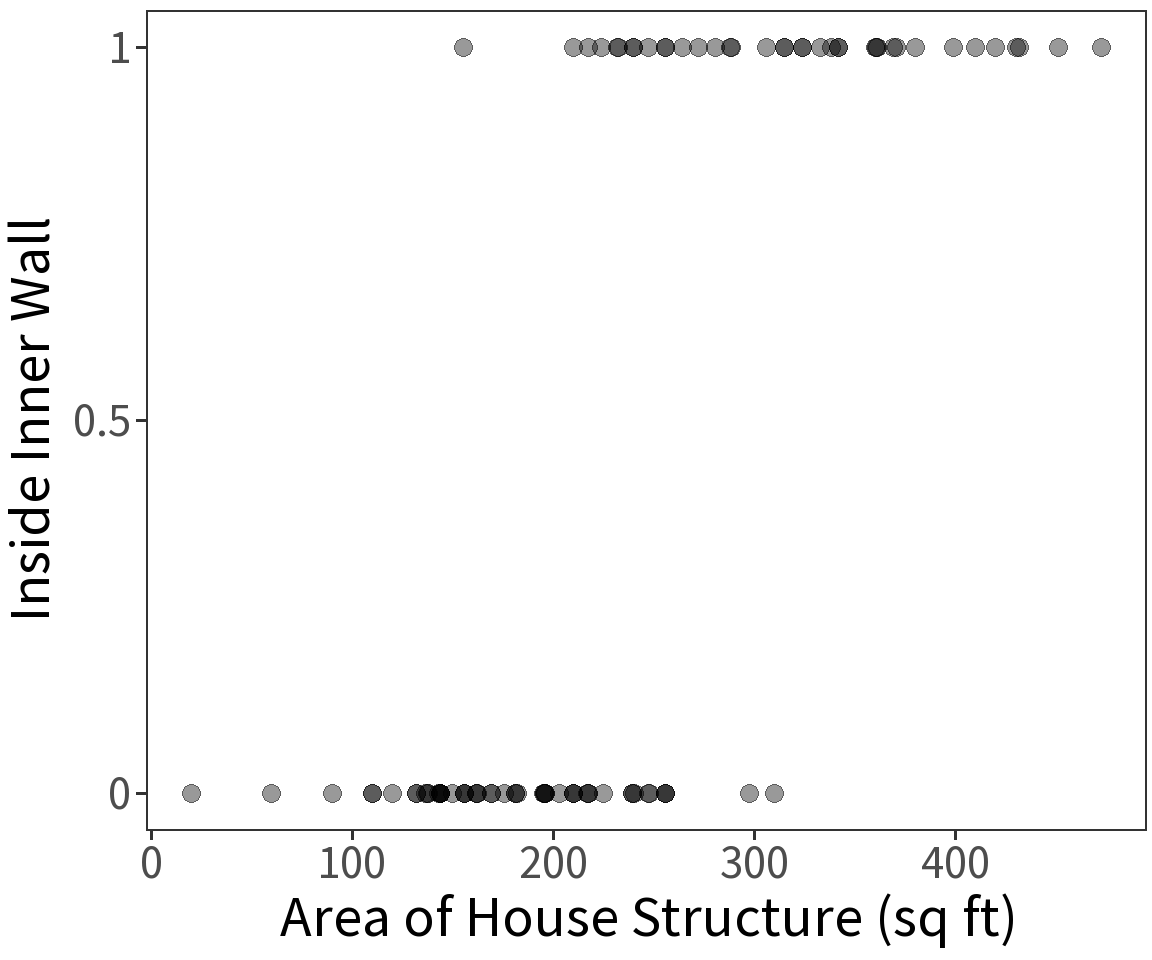
Location inside or outside of the inner wall at the Snodgrass site is a Bernoulli variable and has expectation \(E(Y) = p\) where
\[p = \frac{1}{1 + exp(-\beta X)}\] This defines a logistic curve or sigmoid, with \(p\) being the probability of success. This constrains the estimate \(E(Y)\) to be in the range 0 to 1.
Taking the log of \(p\) gives us
\[log(p) = log\left(\frac{p}{1 - p}\right) = \beta X\]
This is known as the “logit” or log odds.
Question What is the probability that we observe these data (these inside features) given a model with parameters \(\beta\)?
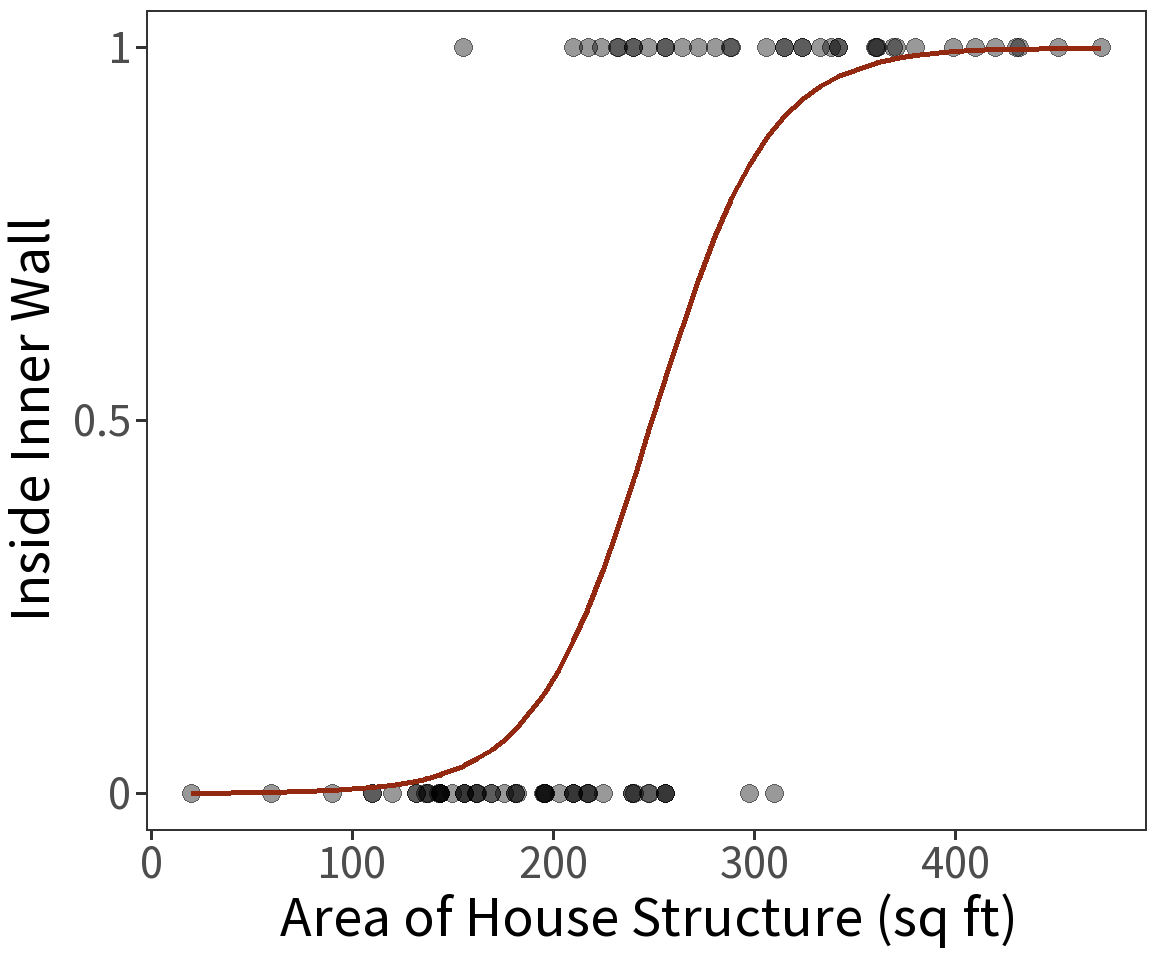
Estimated coefficients:
\(\beta_0 = -8.6631\)
\(\beta_1 = 0.0348\)
For these, the log Likelihood is
\(\mathcal{l} = -28.8641\)
Interpretation
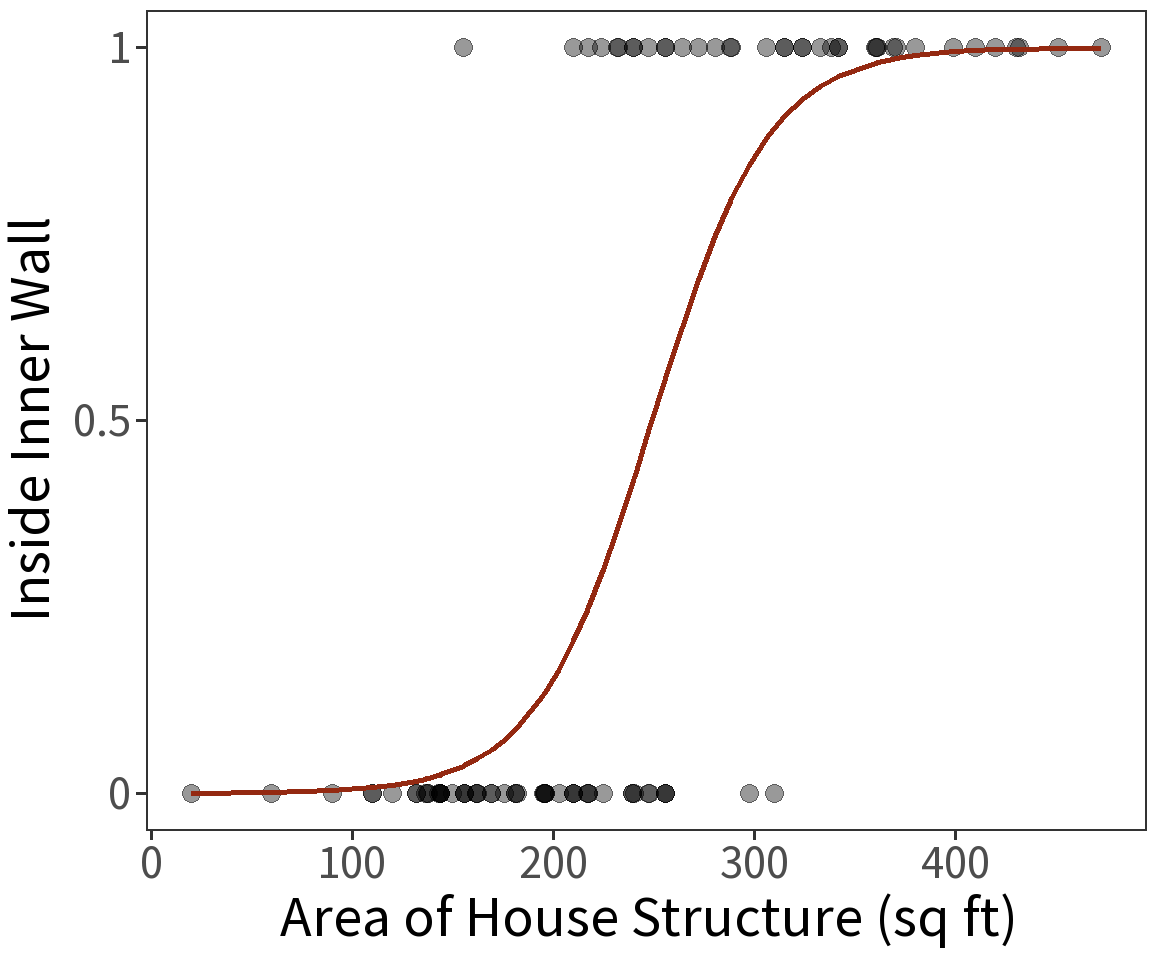
Estimated coefficients:
\(\beta_0 = -8.6631\)
\(\beta_1 = 0.0348\)
Note that these coefficient estimates are log-odds! To get the odds, we take the exponent.
\(\beta_0 = exp(-8.6631) = 0.0002\)
\(\beta_1 = exp(0.0348) = 1.0354\)
For a one unit increase in area, the odds of being in the inside wall increase by 1.0354.
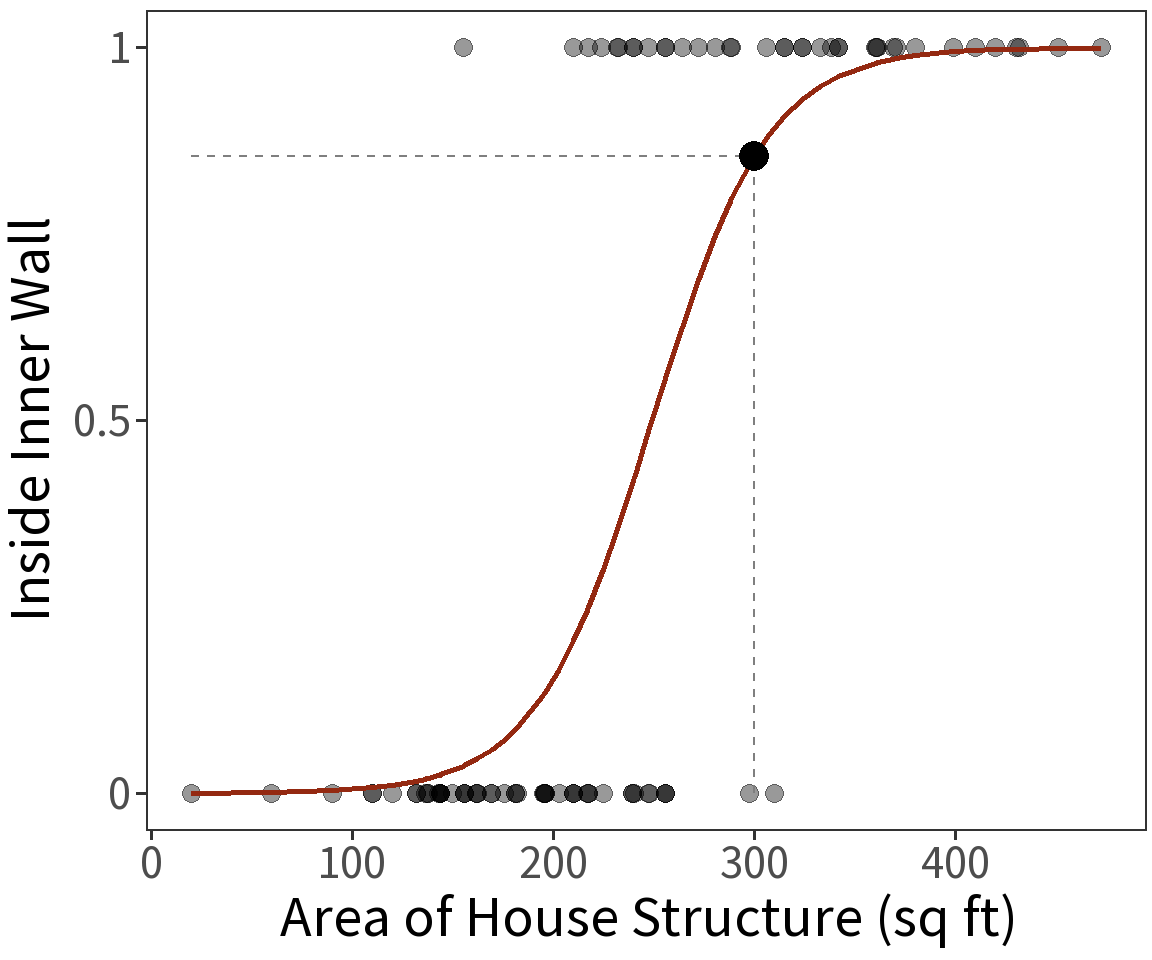
Estimated coefficients:
\(\beta_0 = -8.6631\)
\(\beta_1 = 0.0348\)
To get the probability, we can use the mean function (also known as the inverse link):
\[p = \frac{1}{1+exp(-\beta X)}\]
For a house structure with an area of 300 square feet, the estimated probability that it occurs inside the inner wall is 0.8538.
Proportional response
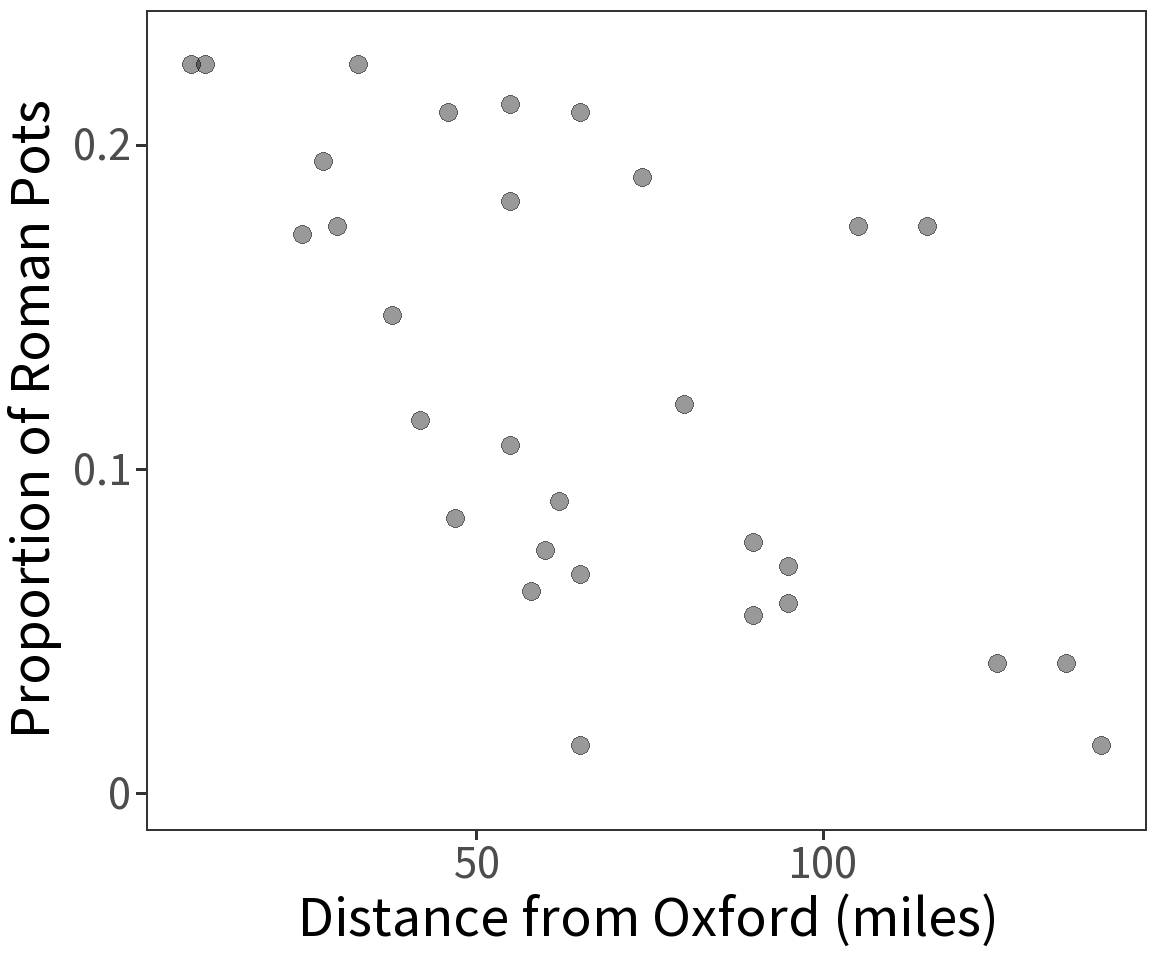
Proportion of Roman pottery is a binomial variable and has expectation \(E(Y) = p\) where
\[p = \frac{1}{1 + exp(-\beta X)}\] This defines a logistic curve or sigmoid, with \(p\) being the proportion of successful Bernoulli trials. This constrains the estimate \(E(Y)\) to be in the range 0 to 1.
Taking the log of \(p\) gives us
\[log(p) = log\left(\frac{p}{1 - p}\right) = \beta X\]
This is known as the “logit” or log odds.
Question What is the probability that we observe these data (these proportions) given a model with parameters \(\beta\)?
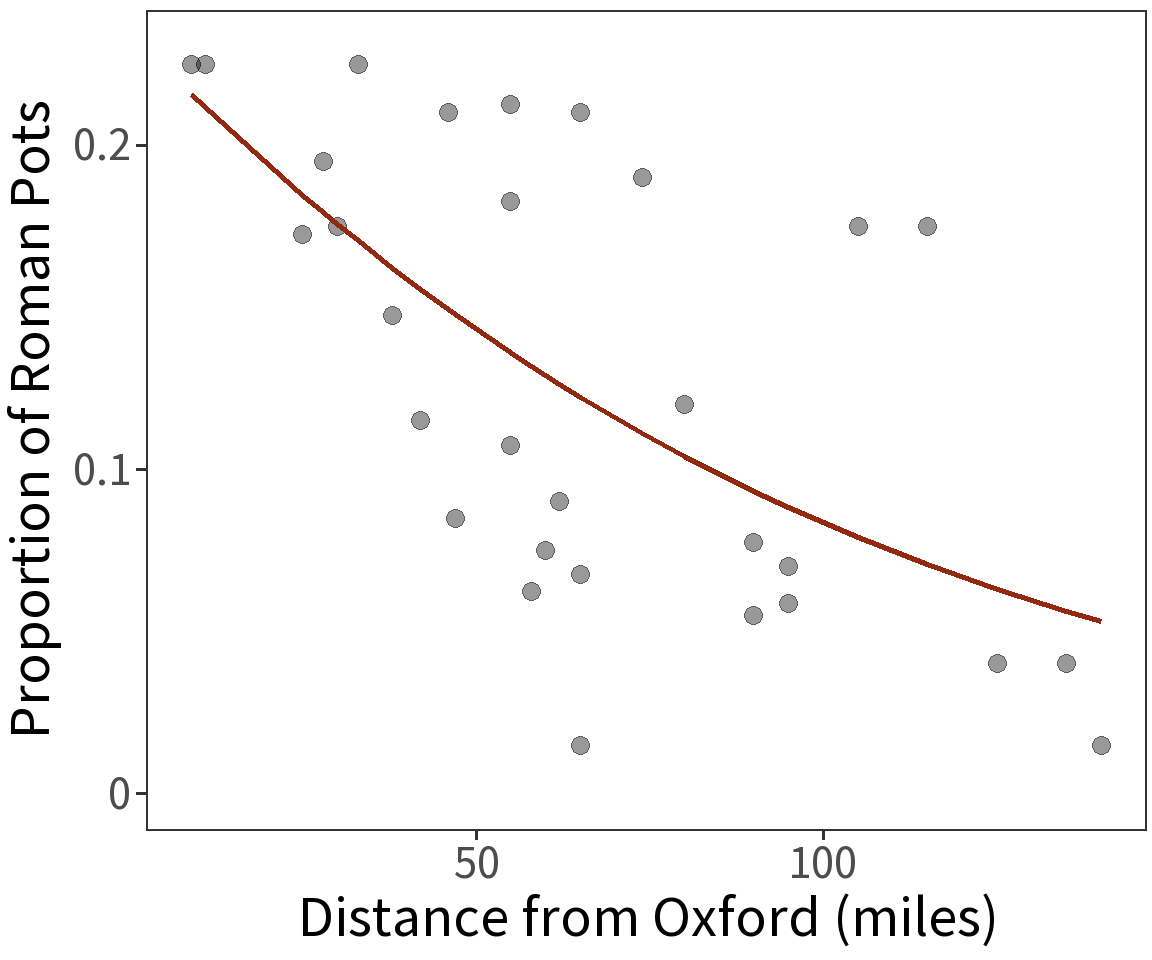
Estimated coefficients:
\(\beta_0 = -1.1818\)
\(\beta_1 = -0.0121\)
For these, the log Likelihood is
\(\mathcal{l} = -4.1148\)
Deviance
- Measure of goodness of fit, so smaller is better
- Gives the difference in log-Likelihood between a model \(M\) and a saturated model \(M_S\)
- \(M_S\) has a parameter for each observation (i.e., zero degrees of freedom)
\[D = -2\,\Big[\,log\,\mathcal{L}(M_1) - log\,\mathcal{L}(M_S)\,\Big]\]
- Residual deviance = deviance of proposed model
- Null deviance = deviance of null model (ie, intercept-only model)
Information Criteria
- A function of the deviance, so smaller is better
- Two penalties:
- \(n\) = number of observations
- \(p\) = number of parameters
- Akaike Information Criteria
- \(AIC = D + 2p\)
- Bayesian Information Criteria
- \(BIC = D + (p \cdot log(n))\)
ANOVA
- Analysis of Deviance aka Likelihood Ratio Test
- For Binomial and Poisson models
- Test statistic is the logged ratio of likelihoods between proposed, \(M_1\), and null, \(M_0\), models
\[ \begin{aligned} \chi^2 &= -2\,log\,\frac{\mathcal{L}(M_0)}{\mathcal{L}(M_1)}\\\\ &= -2\,\Big[\,log\,\mathcal{L}(M_0) - log\,\mathcal{L}(M_1)\,\Big] \end{aligned} \]
- Compare to a \(\chi^2\) distribution with \(k\) degrees of freedom - asks what the probability is of getting a value greater than the observed \(\chi^2\) value.
- Null hypothesis is no difference in log-Likelihood.