Lecture 11: Maximum Likelihood
3/21/23
📋 Lecture Outline
- Limitations of OLS
- Likelihood
- Likelihood Estimation
- Maximum Likelihood Estimation (MLE)
Limitations of OLS
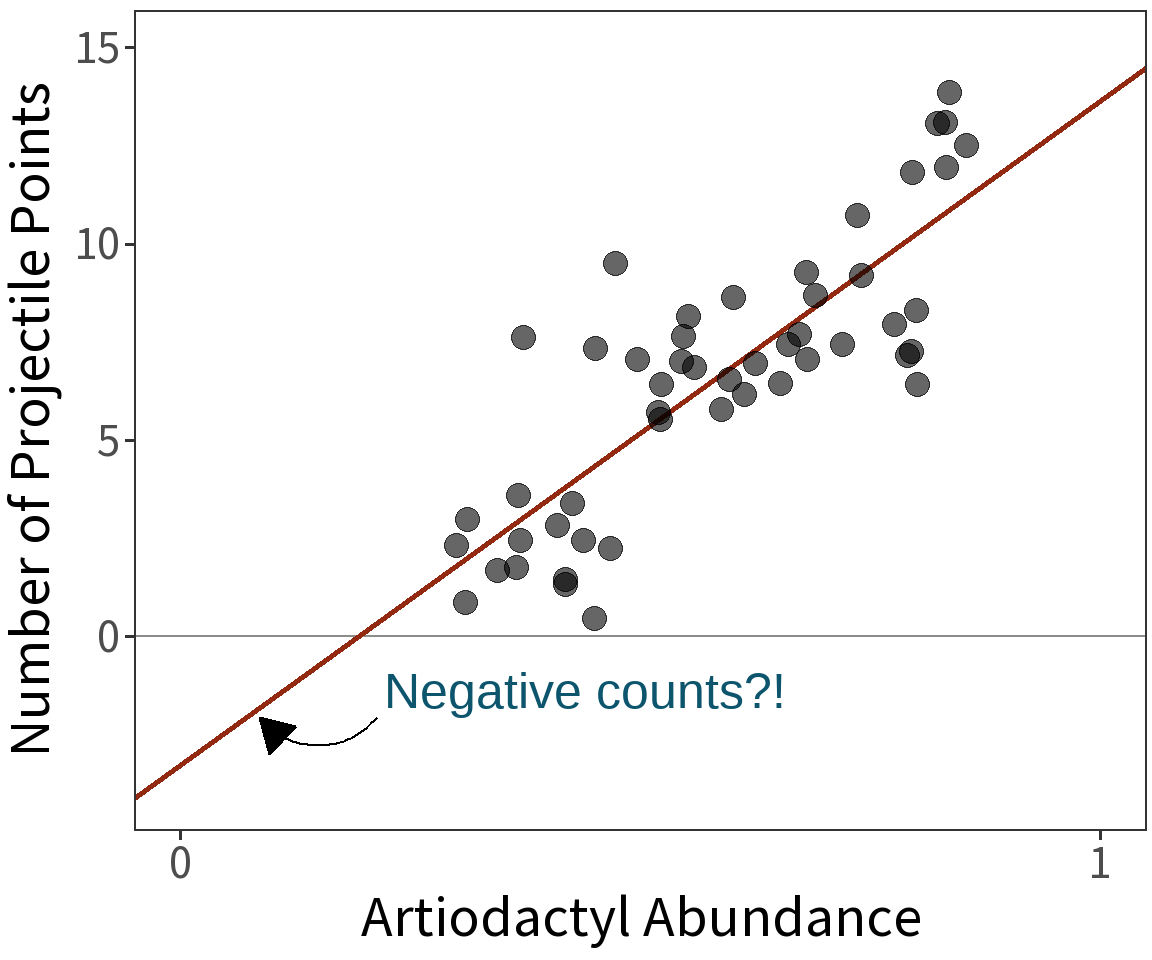
This is a made-up dataset.
Can’t use OLS to model counts or binary outcomes. Inflexible approach to quantifying uncertainty about these types of outcome.
Model evaluation with ANOVA is restricted to subsets.
Likelihood
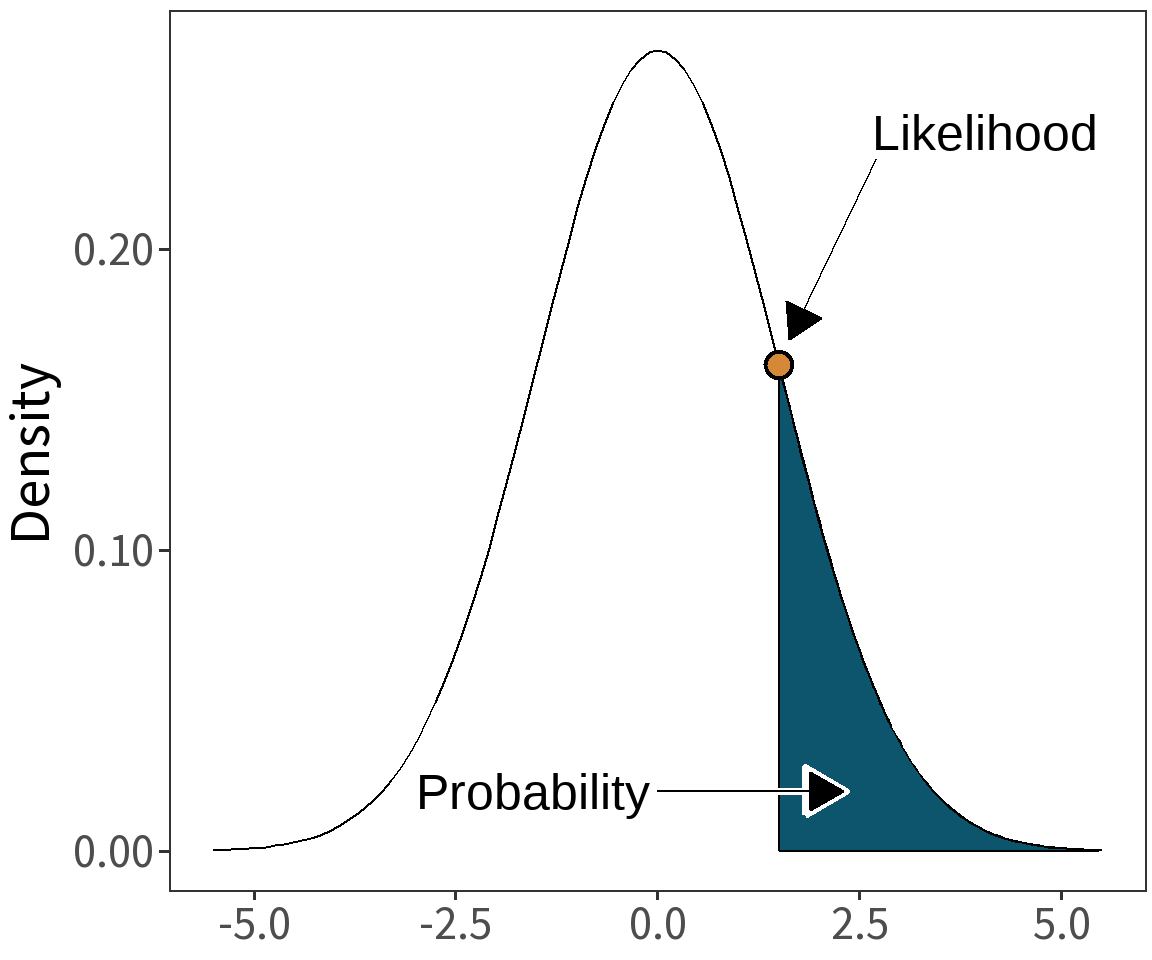
Definition: Probability of data, \(X\), given model, \(\theta\).
\[\mathcal{L}(\theta|X) = P(X|\theta)\]
In English: “The likelihood of the model given the data is equal to the probability of the data given the model.”
Answers the Question: how unlikely or strange is our data?
Likelihood Estimation
A Simple Experiment

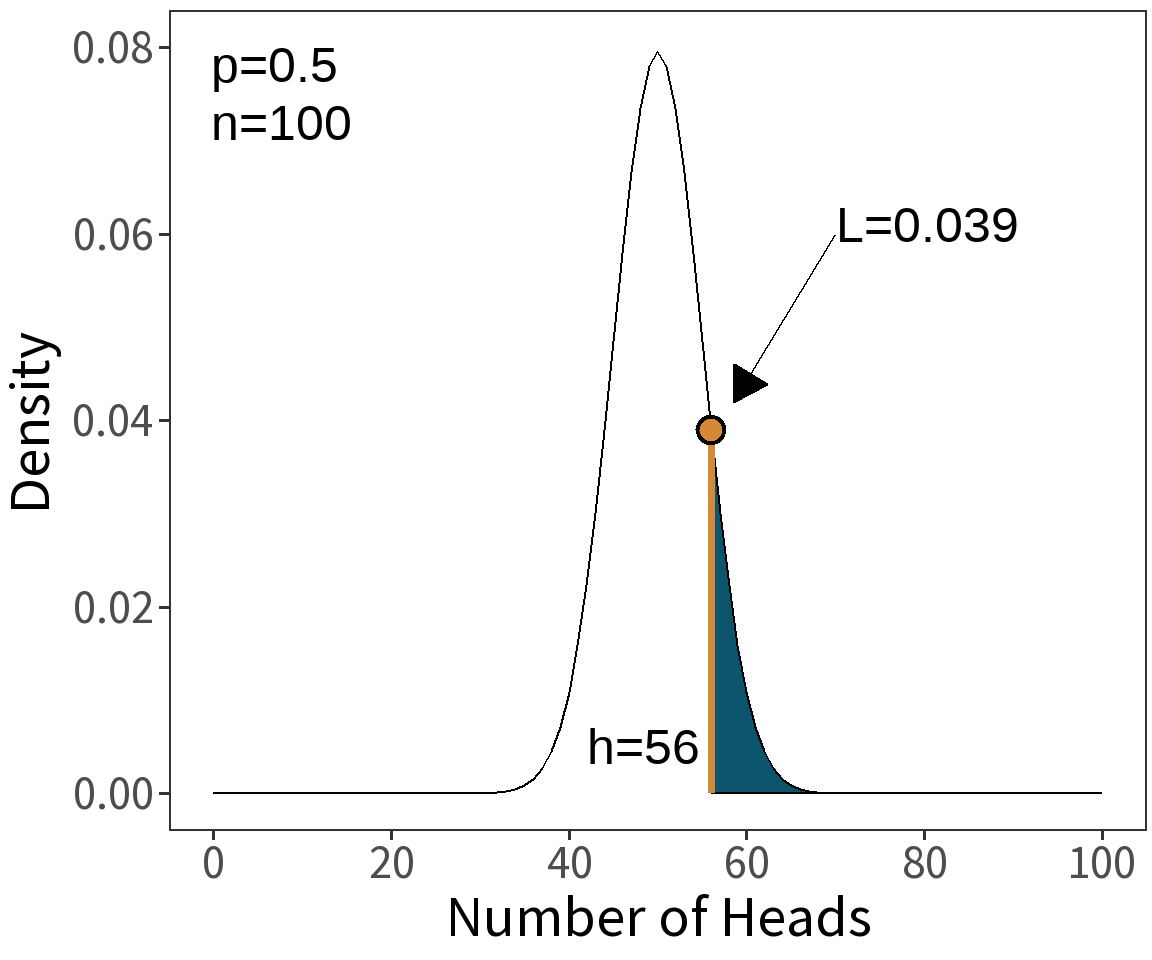
We flip a coin \(n = 100\) times and count the number of heads.
Result: \(h = 56\)
Suppose our model is that the coin is fair.
Question: What is \(\mathcal{L}(p=0.5|h=56)\)?
In English: “How likely is it that the coin is fair given that heads came up 56 times?”
⚠️ This is the probability that heads comes up 56/100 times assuming that the coin is fair.
A Simple Experiment

We flip a coin \(n = 100\) times and count the number of heads.
Result: \(h = 56\)
Suppose our model is that the coin is fair.
Question: What is \(\mathcal{L}(p=0.5|h=56)\)?
This experiment is a series of Bernoulli trials, so we can use the binomial distribution to calculate \(\mathcal{L}(p|h)\).
\[\;\;\;\;\,\mathcal{L}(p|h) = \binom{n}{h}p^{h}(1-p)^{n-h}\]
Suppose our model is that the coin is fair.
Question: What is \(\mathcal{L}(p=0.5|h=56)\)?
This experiment is a series of Bernoulli trials, so we can use the binomial distribution to calculate \(\mathcal{L}(p|h)\).
\[ \begin{align} \mathcal{L}(p=0.5|h=56) &= \binom{100}{56}0.5^{56}(1-0.5)^{100-56}\\\\ \mathcal{L}(p=0.5|h=56) &= 0.039 \end{align} \]
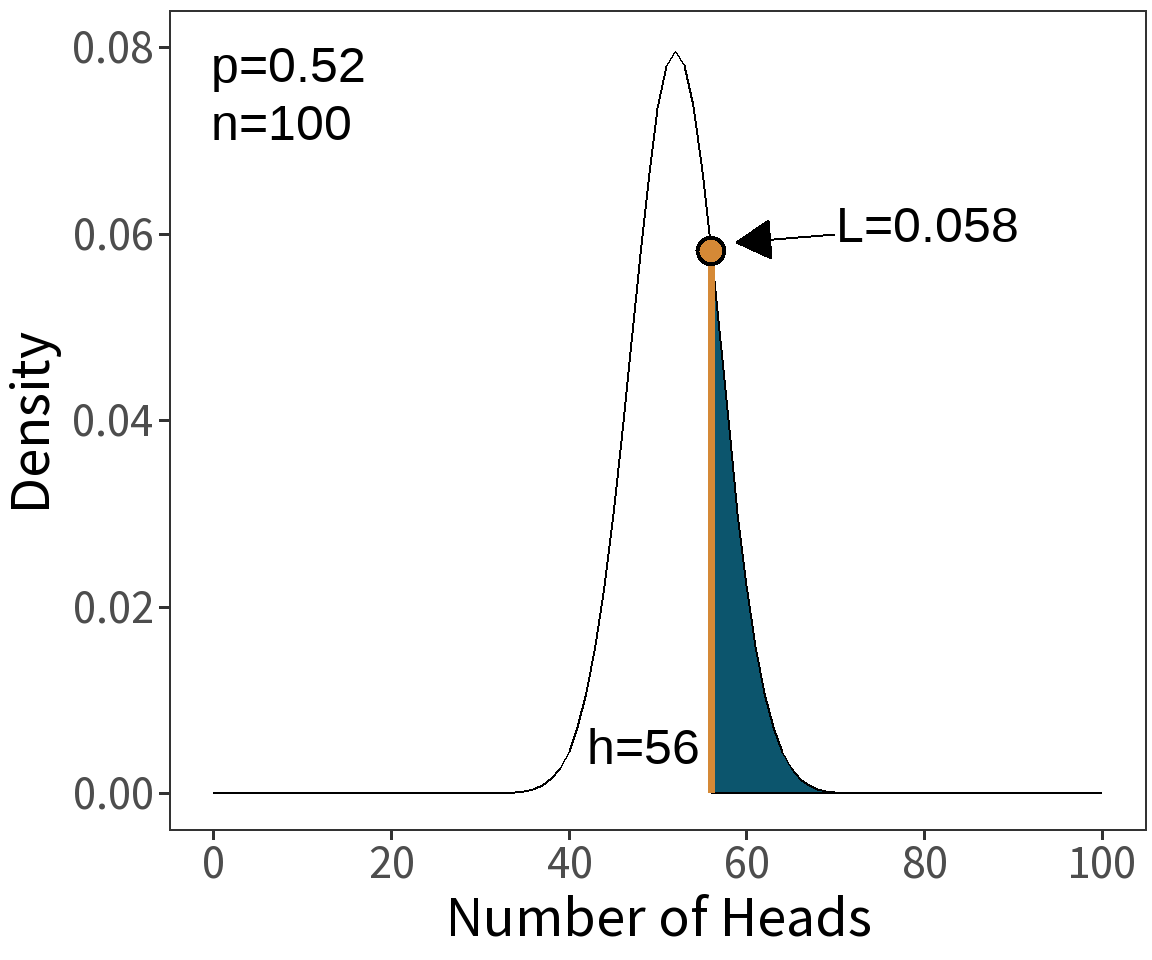
Suppose our model is that the coin is biased.
Question: What is \(\mathcal{L}(p=0.52|h=56)\)?
In English: “How likely is it that the coin is biased given that heads came up 56 times?”
⚠️ This is the probability that heads comes up 56/100 times assuming that the coin is biased.
Maximum Likelihood
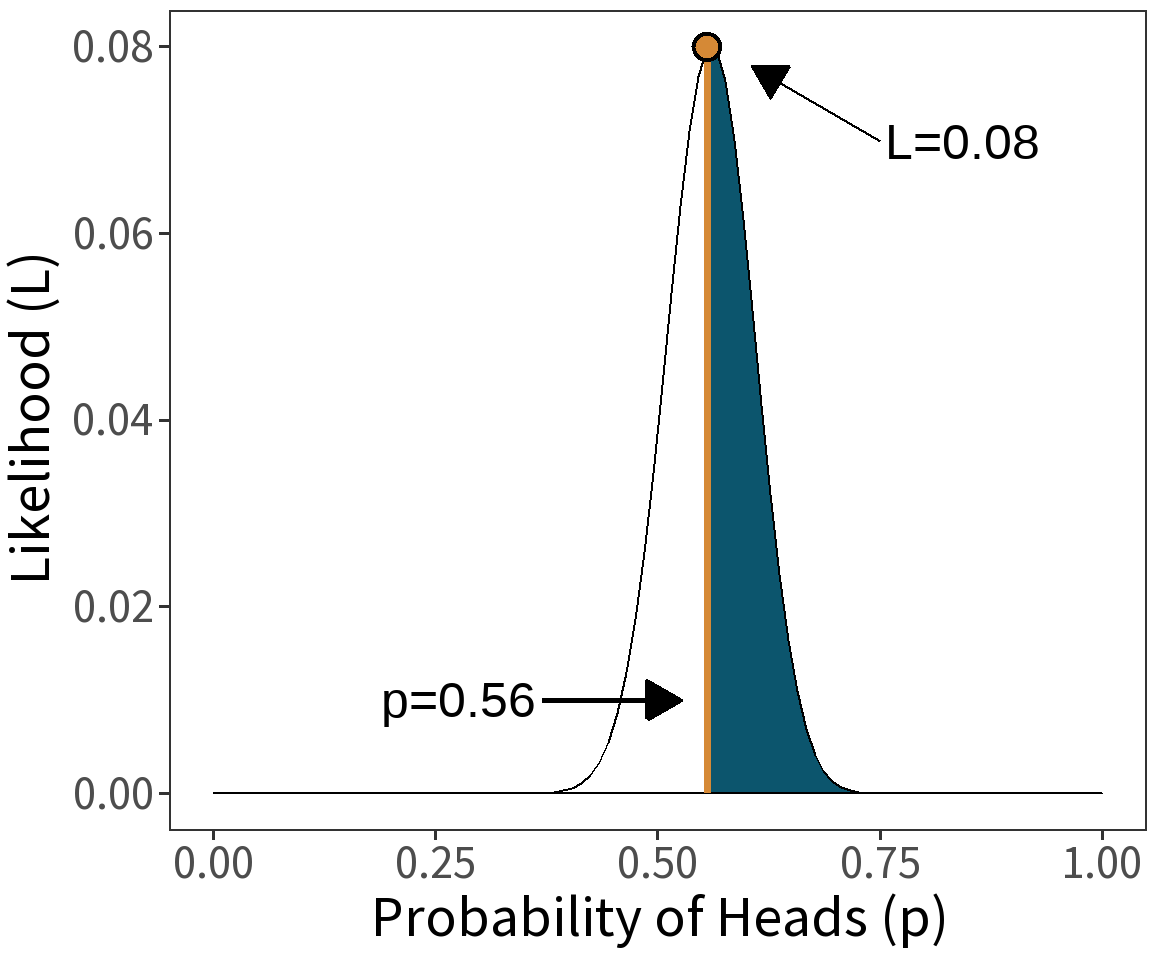
Question: What value of \(p\) maximizes \(\mathcal{L}(p|h)\)?
\[\hat{p} = max\, \mathcal{L}(p|h)\]
In English: “Given a set of models, choose the one that makes what we observe the most probable thing to observe.”
It’s a method for estimating the parameters of a model given some observed data.
Maximum Likelihood Estimation
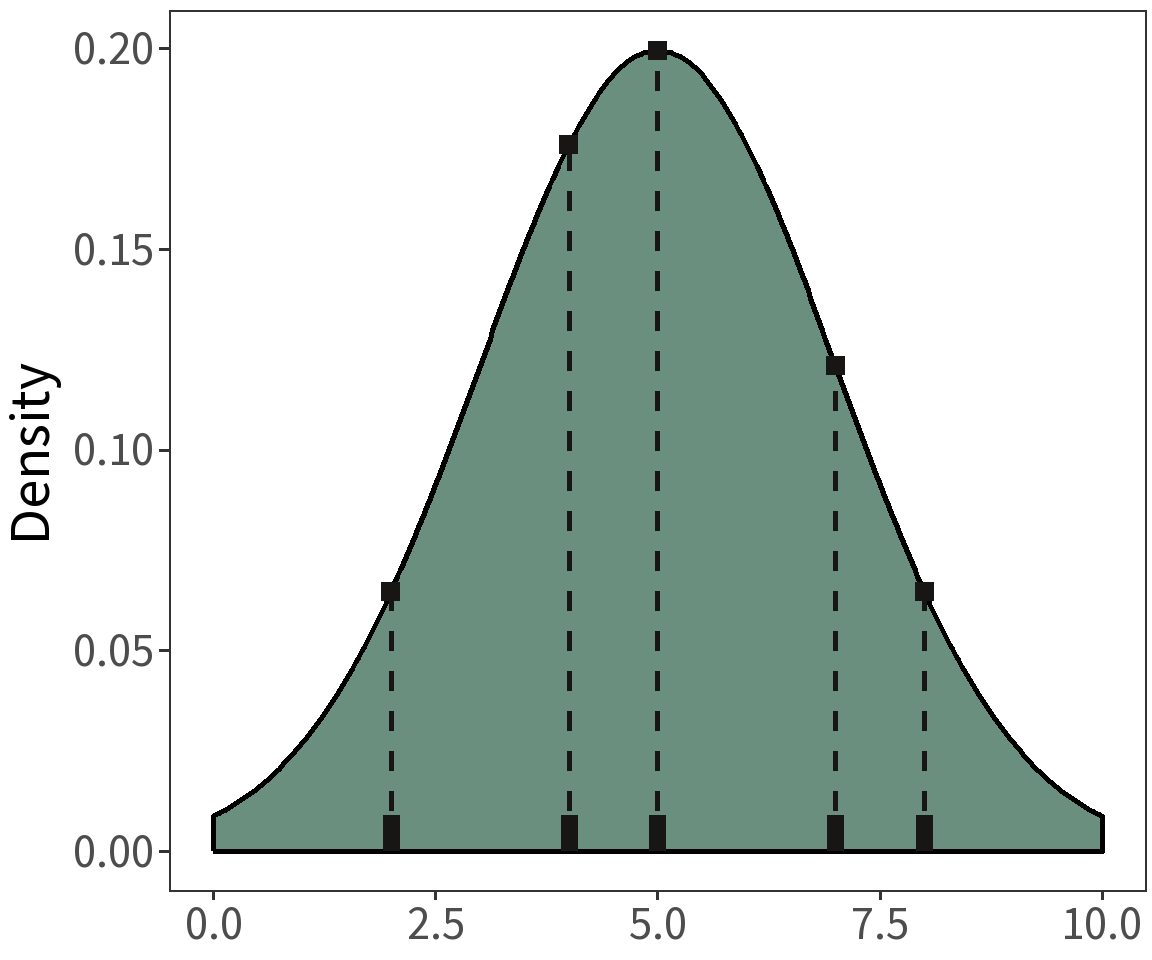
What if we have multiple observations?
\[X = [5, 7, 8, 2, 4]\]
Question: What is the probability that this sample comes from a normal distribution with a mean of 5 and a variance of 2?
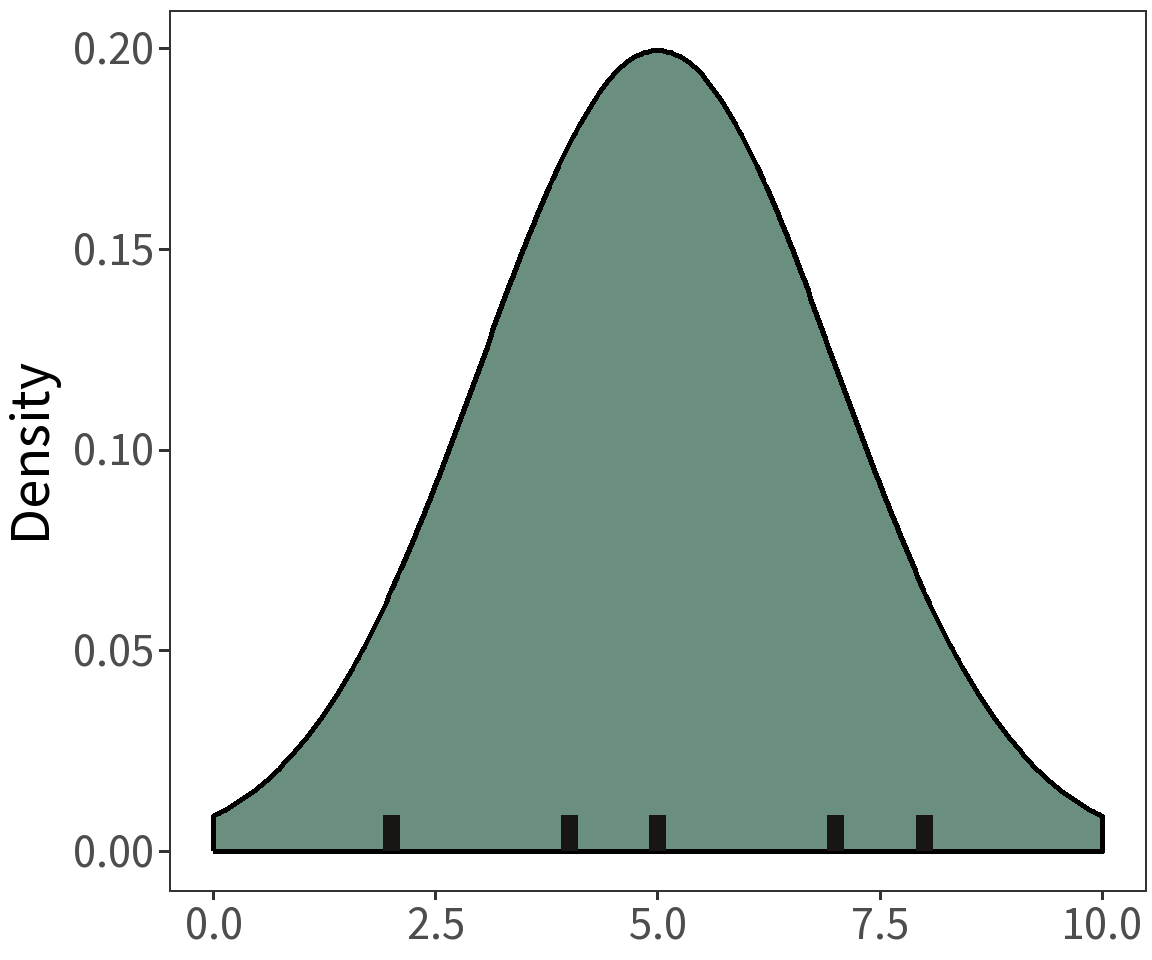
The probability density for a given observation \(x_i\) given a normal distribution is:
\[N(x_i,\mu,\sigma) = \frac{1}{\sqrt{2\pi\sigma^2}}\;exp\left[-\frac{1}{2}\left(\frac{x_i-\mu}{\sigma}\right)^2\right]\]
For any set of values \(X\), the likelihood is the product of the individual densities:
\[\mathcal{L}(\mu, \sigma^2|x_i)=\prod_{i=1}^{n} N(x_i, \mu, \sigma^2)\]
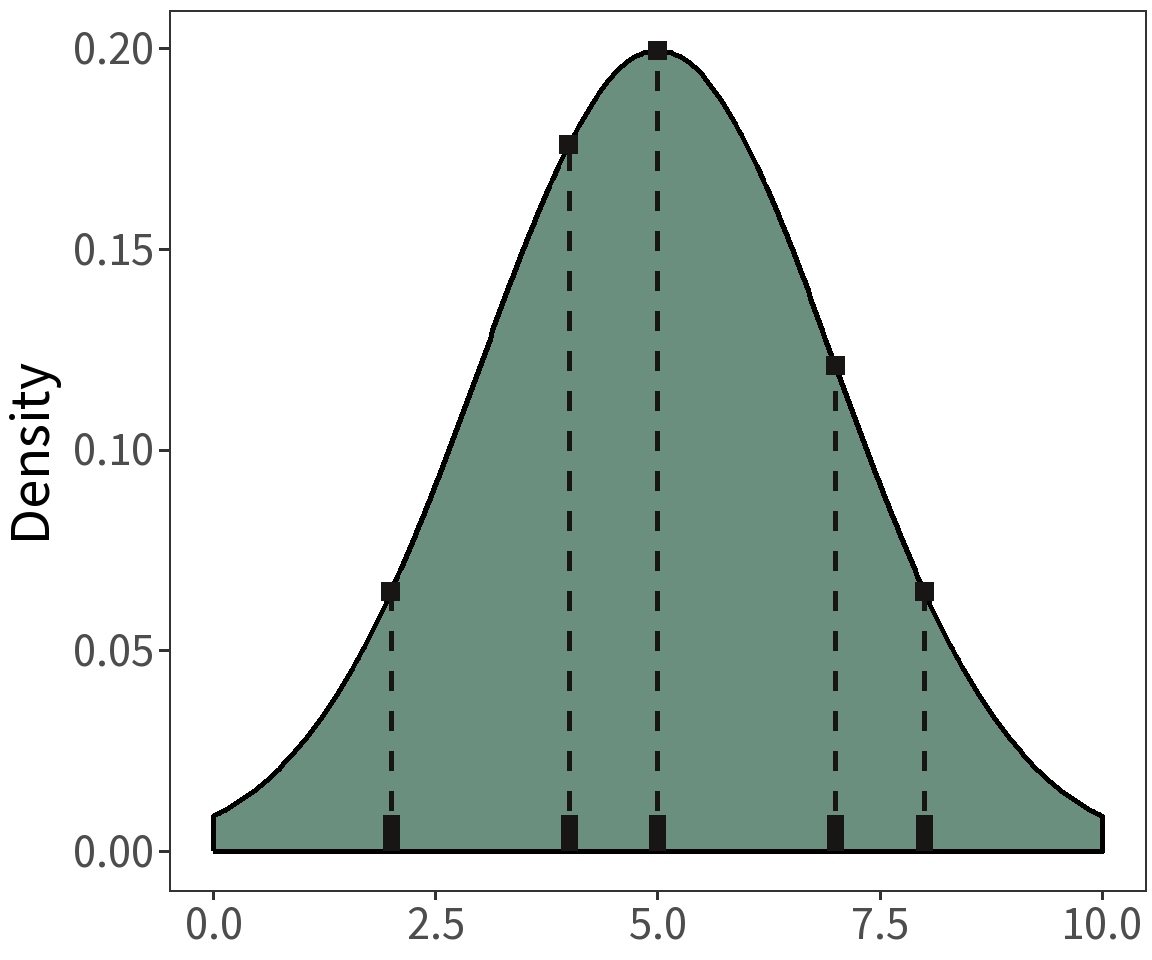
For \(X = [5, 7, 8, 2, 4]\), we have
\[
\begin{align}
\mathcal{L}(\mu, \sigma^2|X) &= N(5) \cdot N(7) \cdot N(8) \cdot N(2) \cdot N(4)\\\\
&= 1.78e-05
\end{align}
\]
where \(\mu=5\) and \(\sigma^2=2\).
As the likelihood is often very small, a common strategy is to minimize the negative log likelihood rather than maximize the likelihood, (\(min\;\mathrm{-}\ell\)) rather than (\(max\;\mathcal{L}\)).