Lecture 10: Transforming Variables

3/14/23

📋 Lecture Outline

• Qualitative variables
  • Dummy variables
  • Intercept offset
  • t-test
• Centering
• Scaling
• Interactions
• Polynomial transformations for non-linearity
• Log transformations for non-linearity

Qualitative Variables

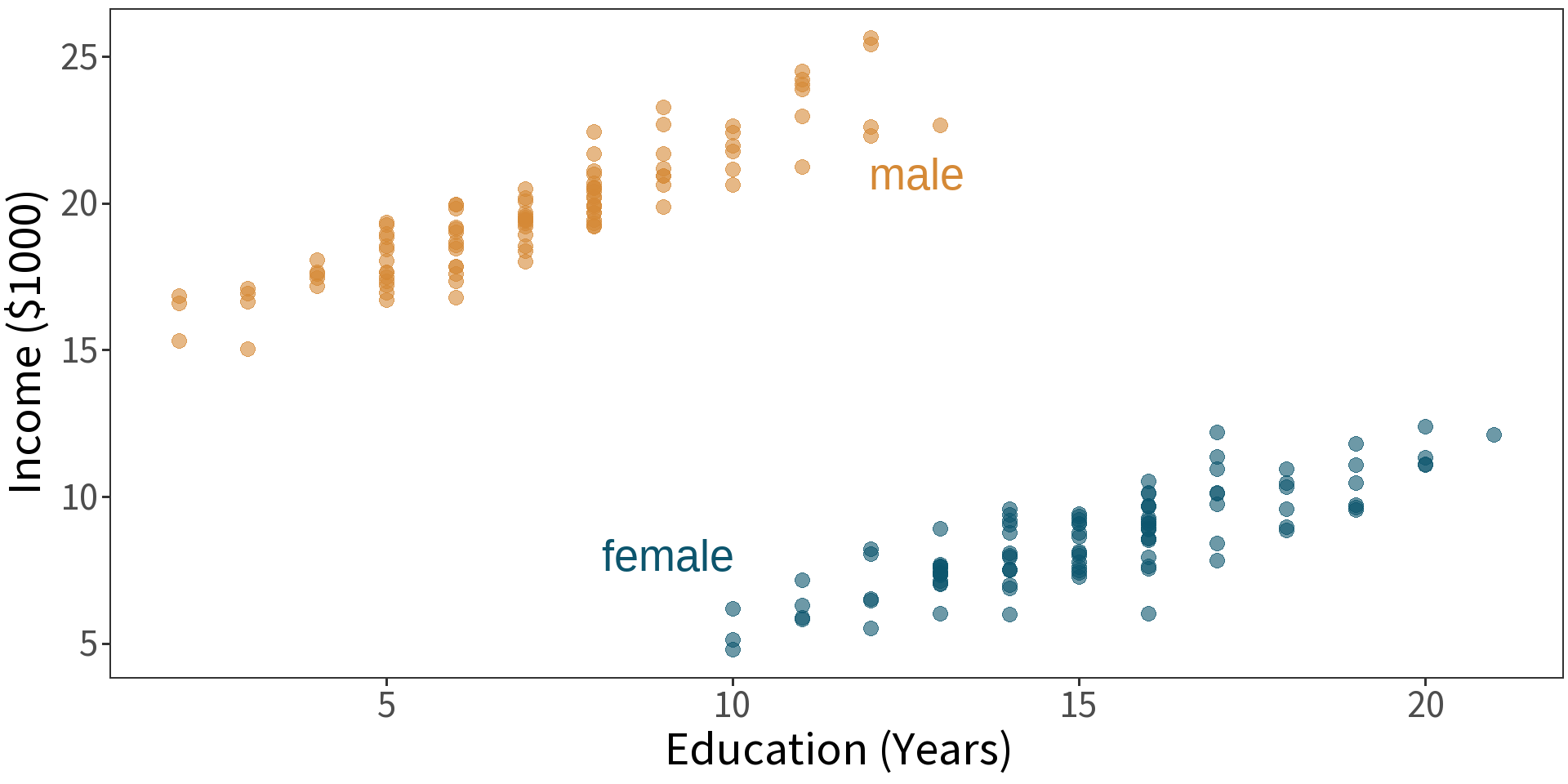
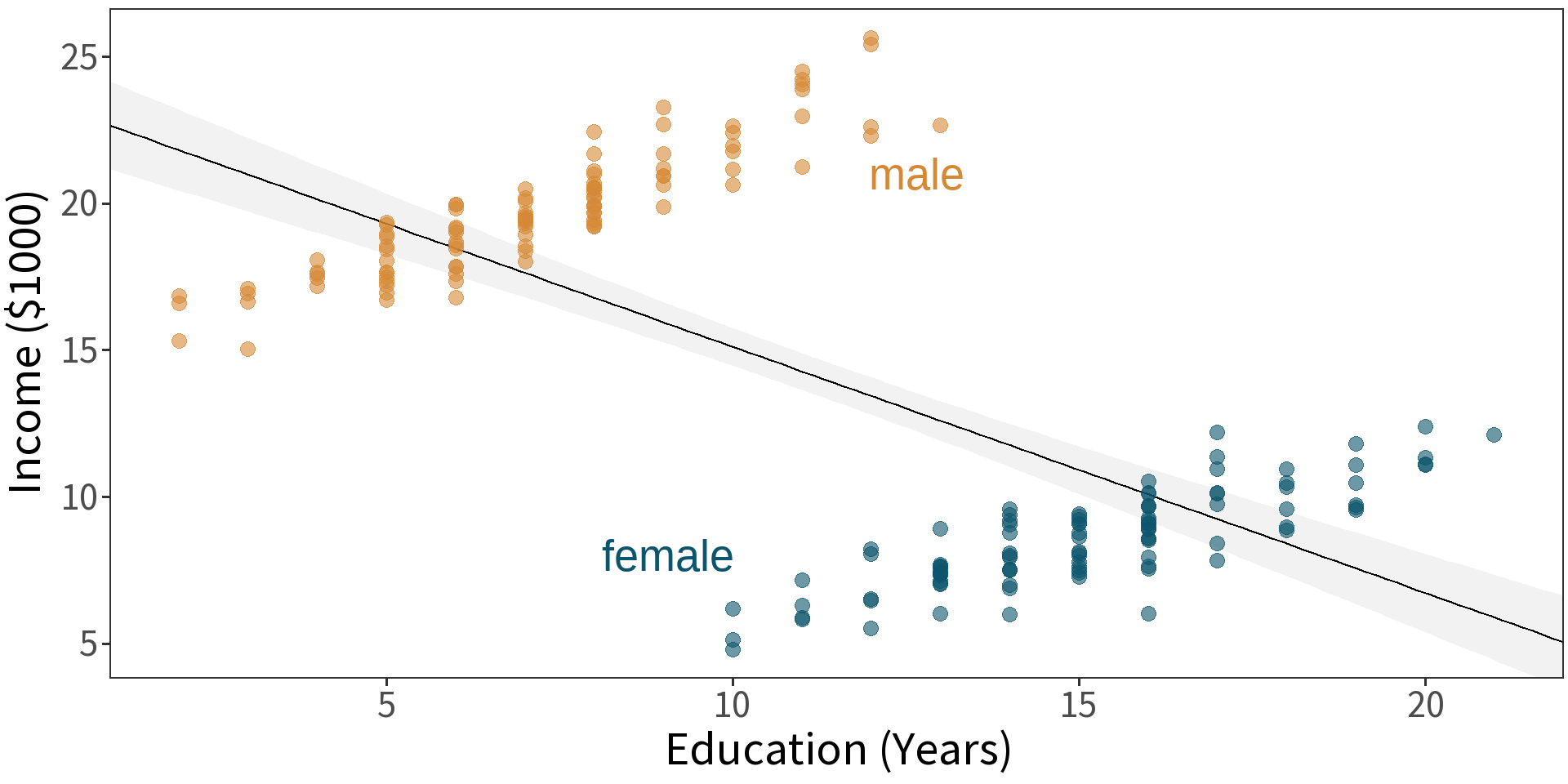
term	estimate	std.error	t.statistic	p.value
Sex Insensitive Model
(Intercept)	23.495	0.809	29.04	0
education	-0.839	0.067	-12.54	0

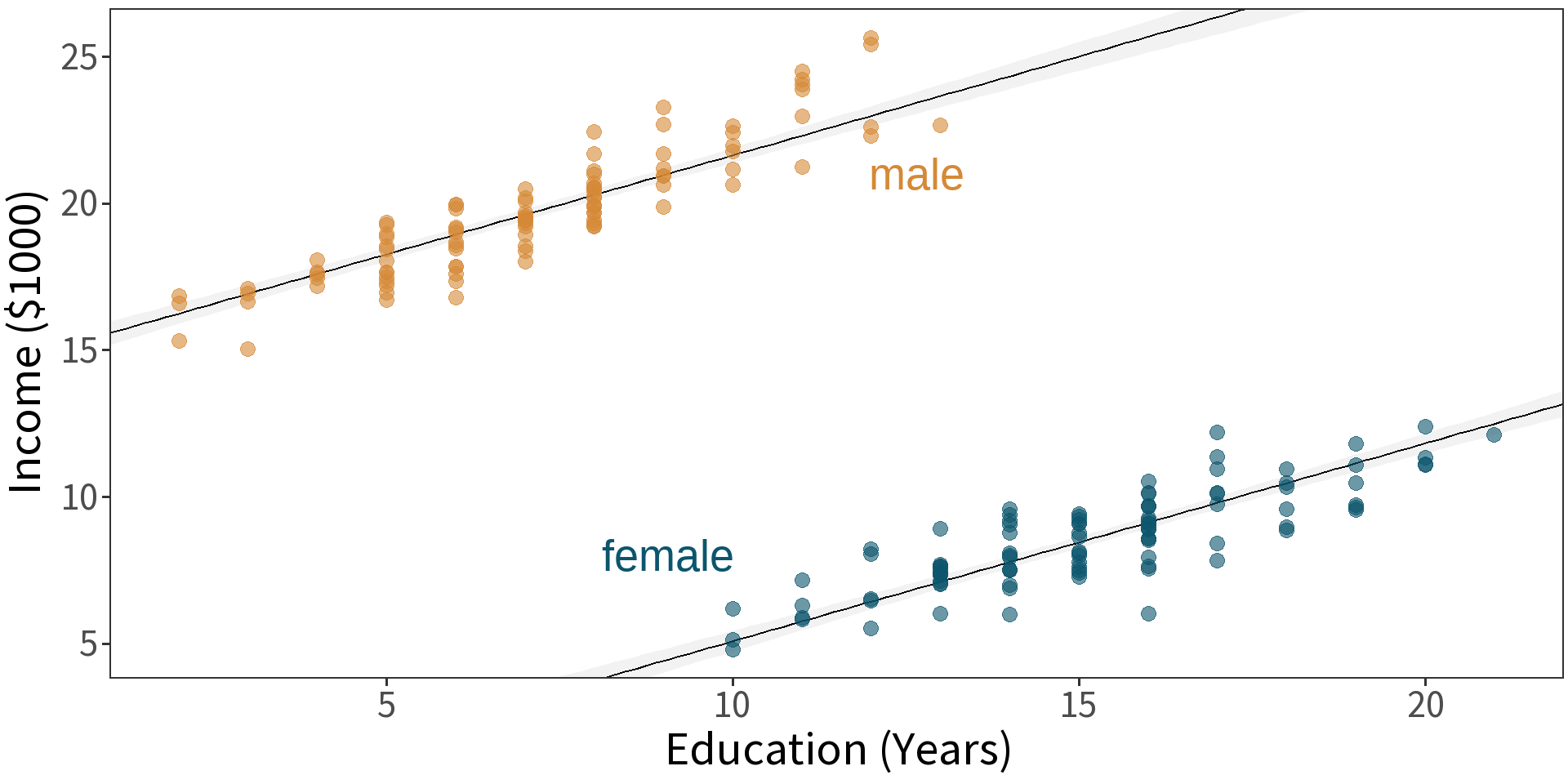
term	estimate	std.error	t.statistic	p.value
Sex Insensitive Model
(Intercept)	23.495	0.809	29.036	0
education	-0.839	0.067	-12.540	0
Sex Sensitive Model
(Intercept)	-1.660	0.441	-3.761	0
education	0.674	0.028	23.732	0
sex(male)	16.556	0.266	62.311	0

Dummy Variables

Dummy variables code each observation:

\(x_i=\left\{\begin{array}{c l} 1 & \text{if i in category} \\ 0 & \text{if i not in category} \end{array}\right.\)

with zero being the reference class.

For m categories, requires m-1 dummy variables.

Category	D1	D2	…	Dm-1
D1	1	0	0	0
D2	0	1	0	0
⋮	⋮	⋮	⋮	⋮
Dm-1	0	0	0	1
Dm	0	0	0	0

Dummy variables code each observation:

\(sex_i=\left\{\begin{array}{c l} 1 & \text{if i-th person is male} \\ 0 & \text{if i-th person is not male} \end{array}\right.\)

Here the reference class is female.

The sex variable has two categories, hence one dummy variable.

sex	male
male	1
female	0
⋮	⋮
male	1
female	0

Intercept Offset

Simple linear model	\(y_i = \beta_0 + \beta_1x_1 + \epsilon_i\)
Add dummy \(D\) with \(\gamma\) offset	\(y_i = (\beta_0 + \gamma\cdot D) + \beta_1x_1 + \epsilon_i\)
for a binary class:
Model for reference class	\(y_i = (\beta_0 + \gamma\cdot 0) + \beta_1x_1 + \epsilon_i\)
Model for other class	\(y_i = (\beta_0 + \gamma\cdot 1) + \beta_1x_1 + \epsilon_i\)

t-test

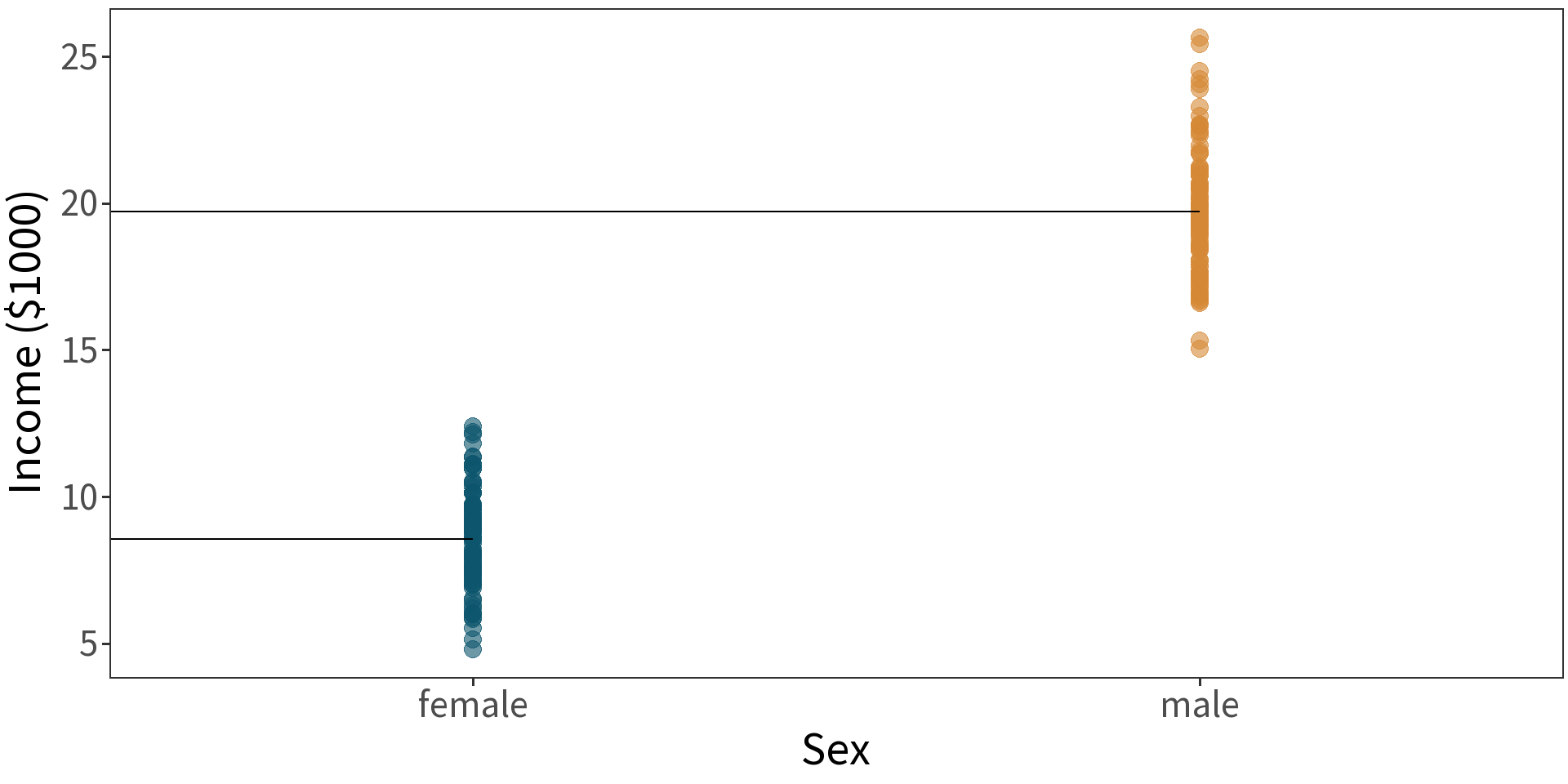
term	estimate	std.error	t.statistic	p.value
Sex Sensitive Model
(Intercept)	8.555	0.191	44.79	0
sex(male)	11.165	0.270	41.33	0

\(H_{0}\): no difference in mean

model: \(income \sim sex\)

\(\bar{y}_{F} = 8.555\)
\(\bar{y}_{M} = \bar{y}_{F} + 11.165 = 19.72\)

Centering

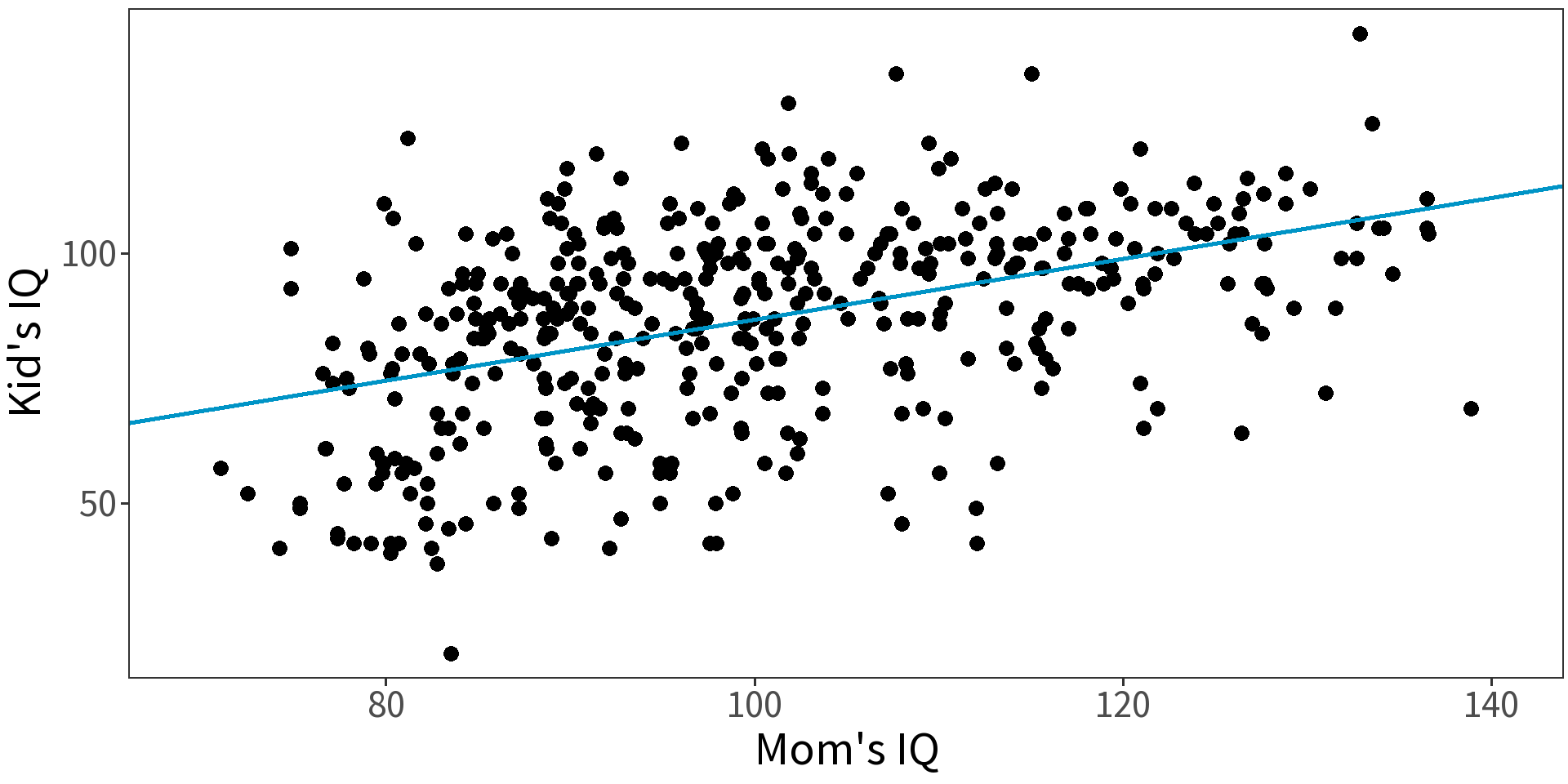
term	estimate	std.error	t.statistic	p.value
Uncentered Model
(Intercept)	25.80	5.917	4.36	0
Mom's IQ	0.61	0.059	10.42	0

Model child IQ as a function of mother’s IQ.

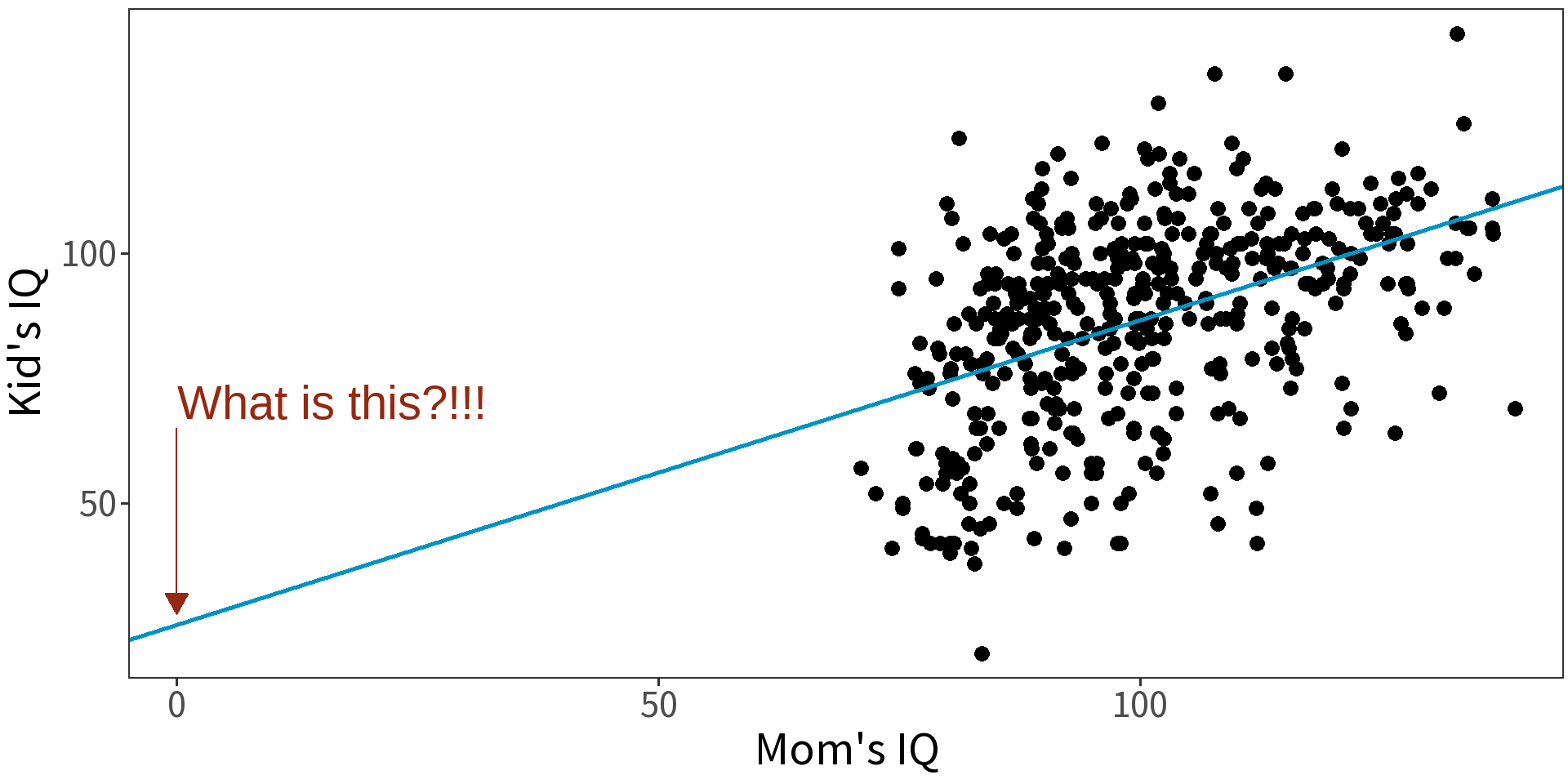
term	estimate	std.error	t.statistic	p.value
Uncentered Model
(Intercept)	25.80	5.917	4.36	0
Mom's IQ	0.61	0.059	10.42	0

Model child IQ as a function of mother’s IQ.

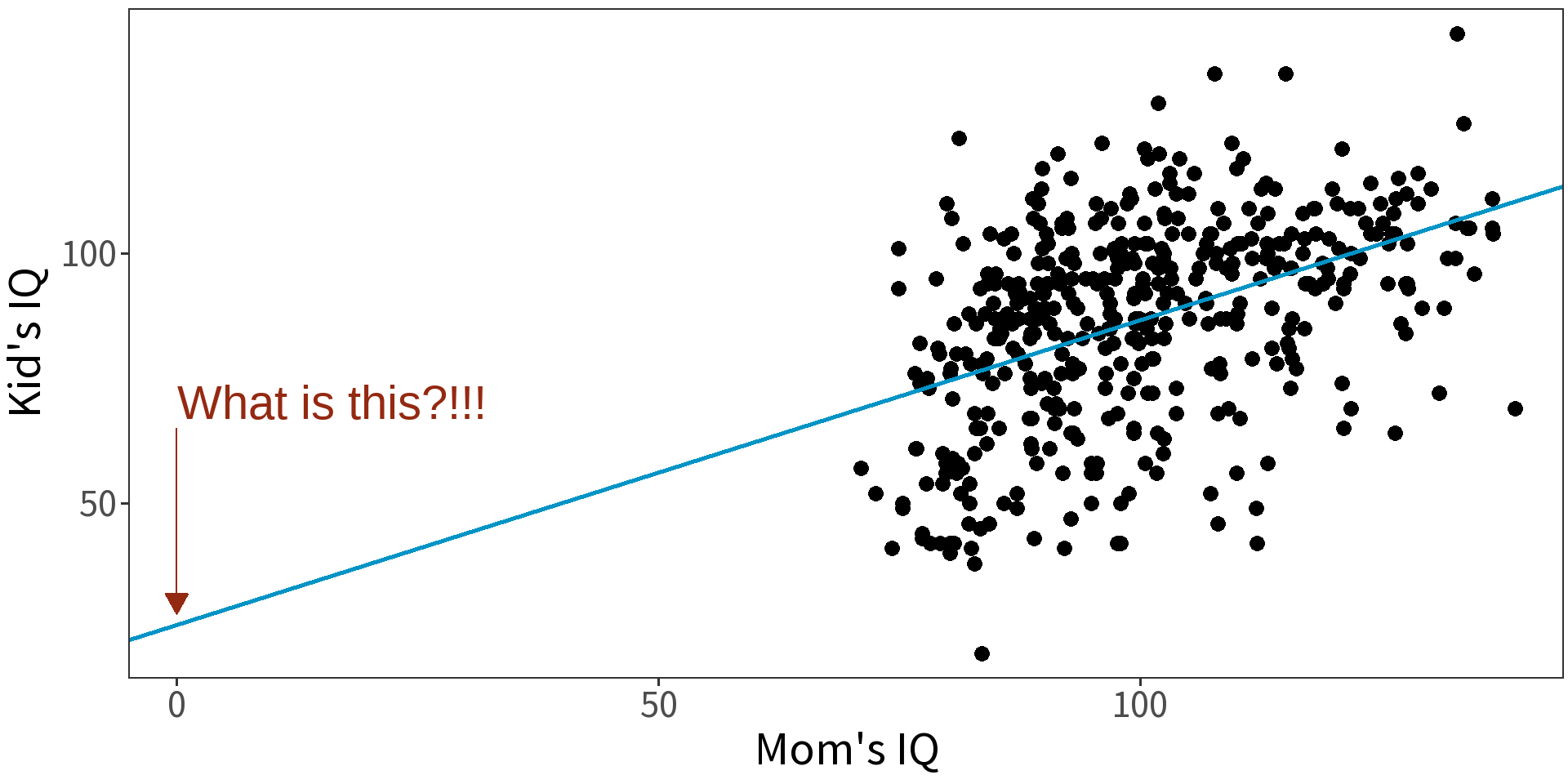
Centering will make intercept more interpretable.

To center, subtract the mean:

\[\text{Mom's IQ} - \text{mean(Mom's IQ)}\]

That gets us this model…

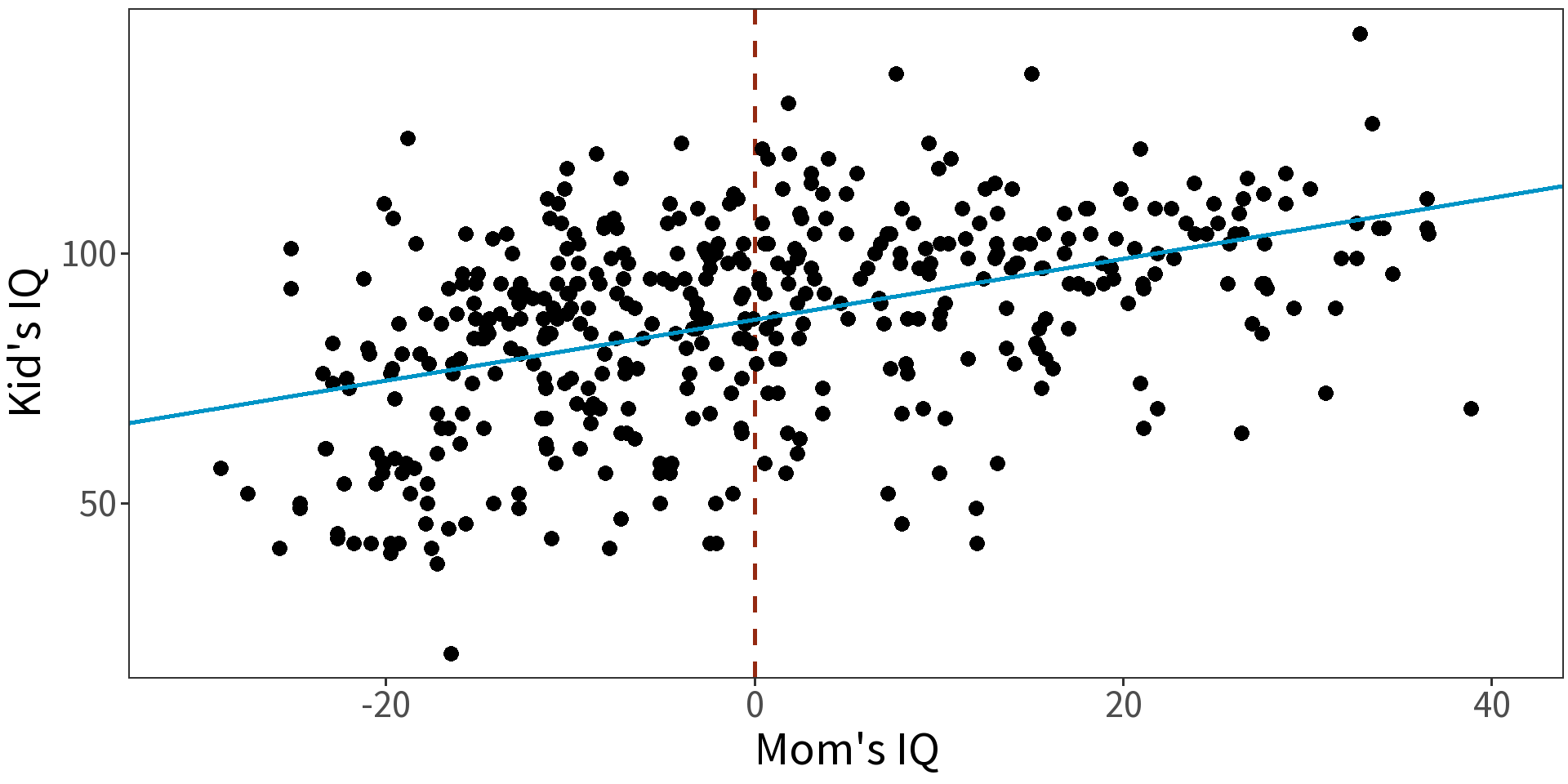
term	estimate	std.error	t.statistic	p.value
Uncentered Model
(Intercept)	25.80	5.917	4.36	0
Mom's IQ	0.61	0.059	10.42	0
Centered Model
(Intercept)	86.80	0.877	98.99	0
Mom's IQ	0.61	0.059	10.42	0

Now we interpret the intercept as expected IQ of a child for a mother with mean IQ. (Notice change in standard error!)

No commitment here to IQ being meaningful. Just an example I’m using till I have time to find a better one.

Scaling

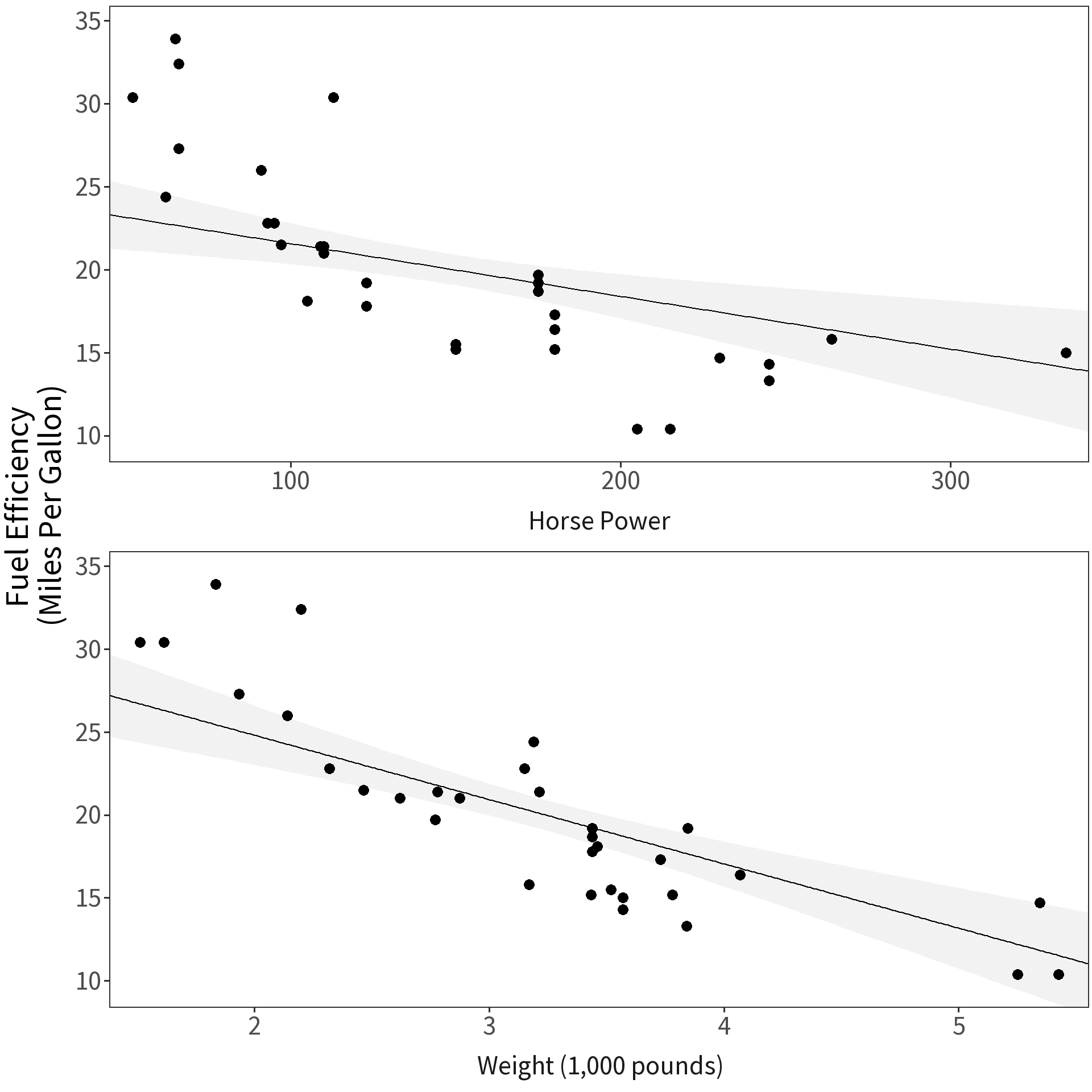
term	estimate	std.error	t.statistic	p.value
Unscaled Model
(Intercept)	37.227	1.599	23.285	0.000
Horsepower	-0.032	0.009	-3.519	0.001
Weight	-3.878	0.633	-6.129	0.000

Model fuel efficiency as a function of weight and horse power.

Question Which covariate has a bigger effect?

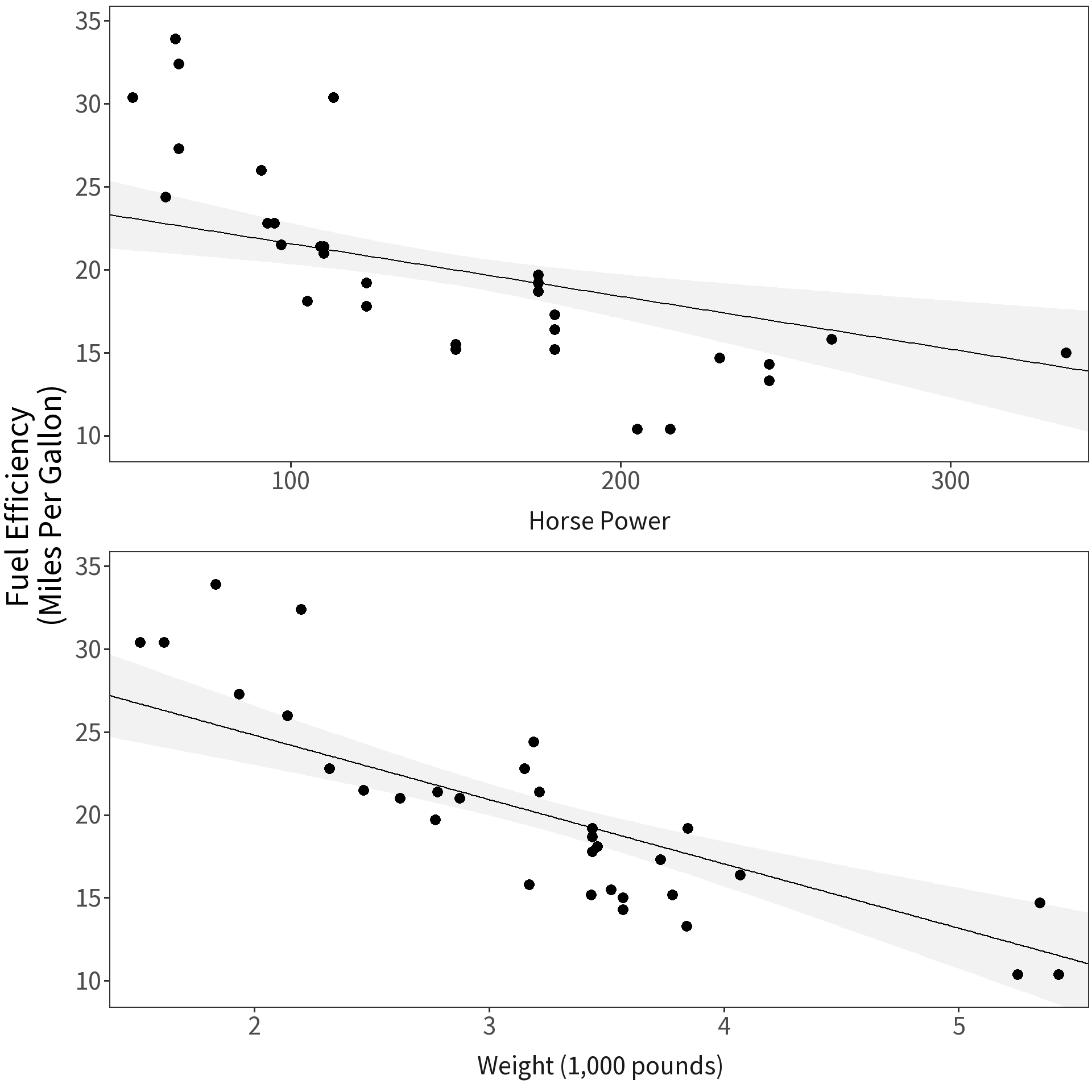
Problem Cannot directly compare coefficients on different scales.

Solution Convert variable values to their z-scores:

\[z_i = \frac{x_i-\bar{x}}{\sigma_{x}}\]

All coefficients now give change in \(y\) for 1\(\sigma\) change in \(x\).

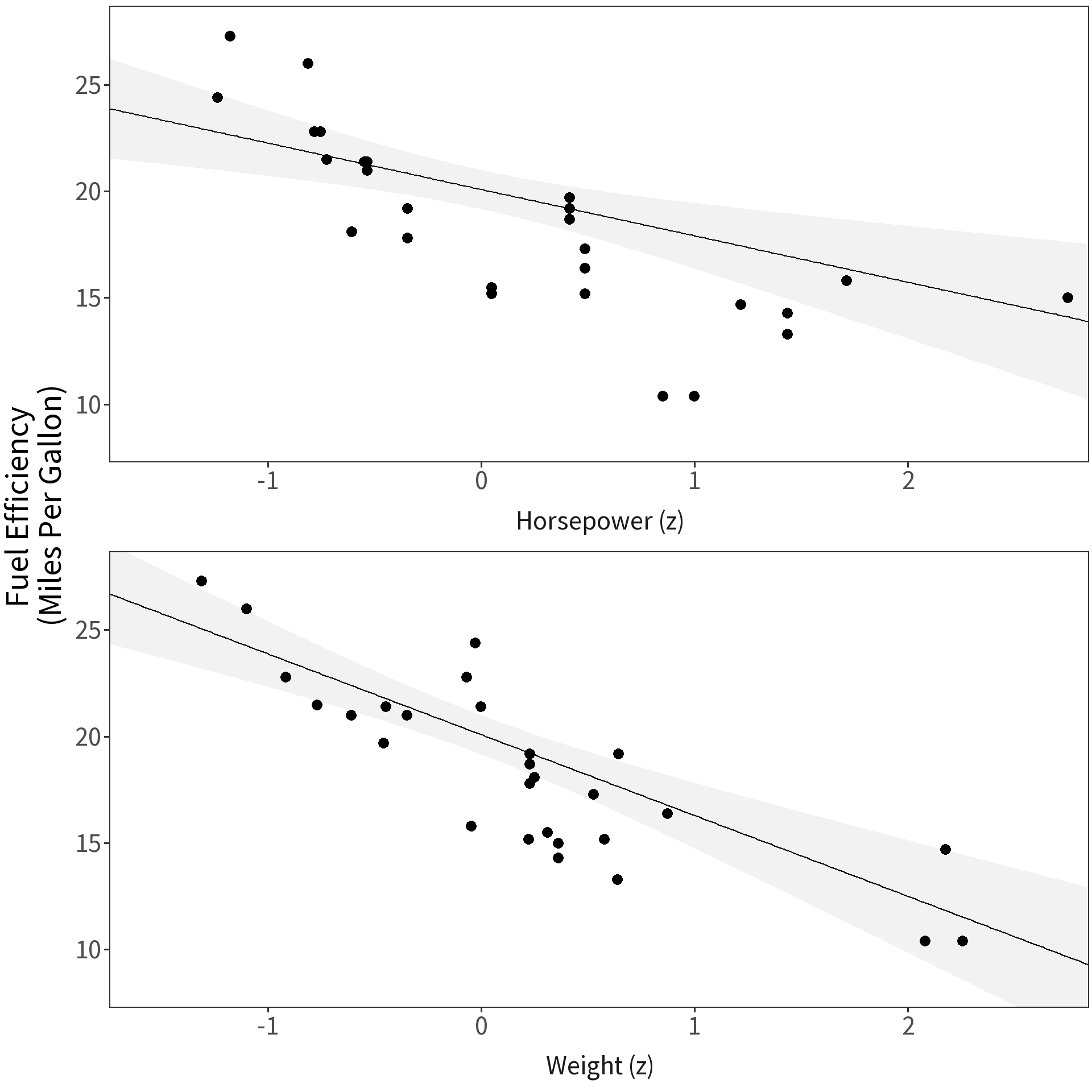
term	estimate	std.error	t.statistic	p.value
Unscaled Model
(Intercept)	37.227	1.599	23.285	0.000
Horsepower	-0.032	0.009	-3.519	0.001
Weight	-3.878	0.633	-6.129	0.000
Scaled Model
(Intercept)	20.091	0.458	43.822	0.000
Horsepower	-2.178	0.619	-3.519	0.001
Weight	-3.794	0.619	-6.129	0.000

Interactions

term	estimate	std.error	t.statistic	p.value
Additive Model
(Intercept)	86.80	0.877	98.99	0
Mom's IQ	0.61	0.059	10.42	0

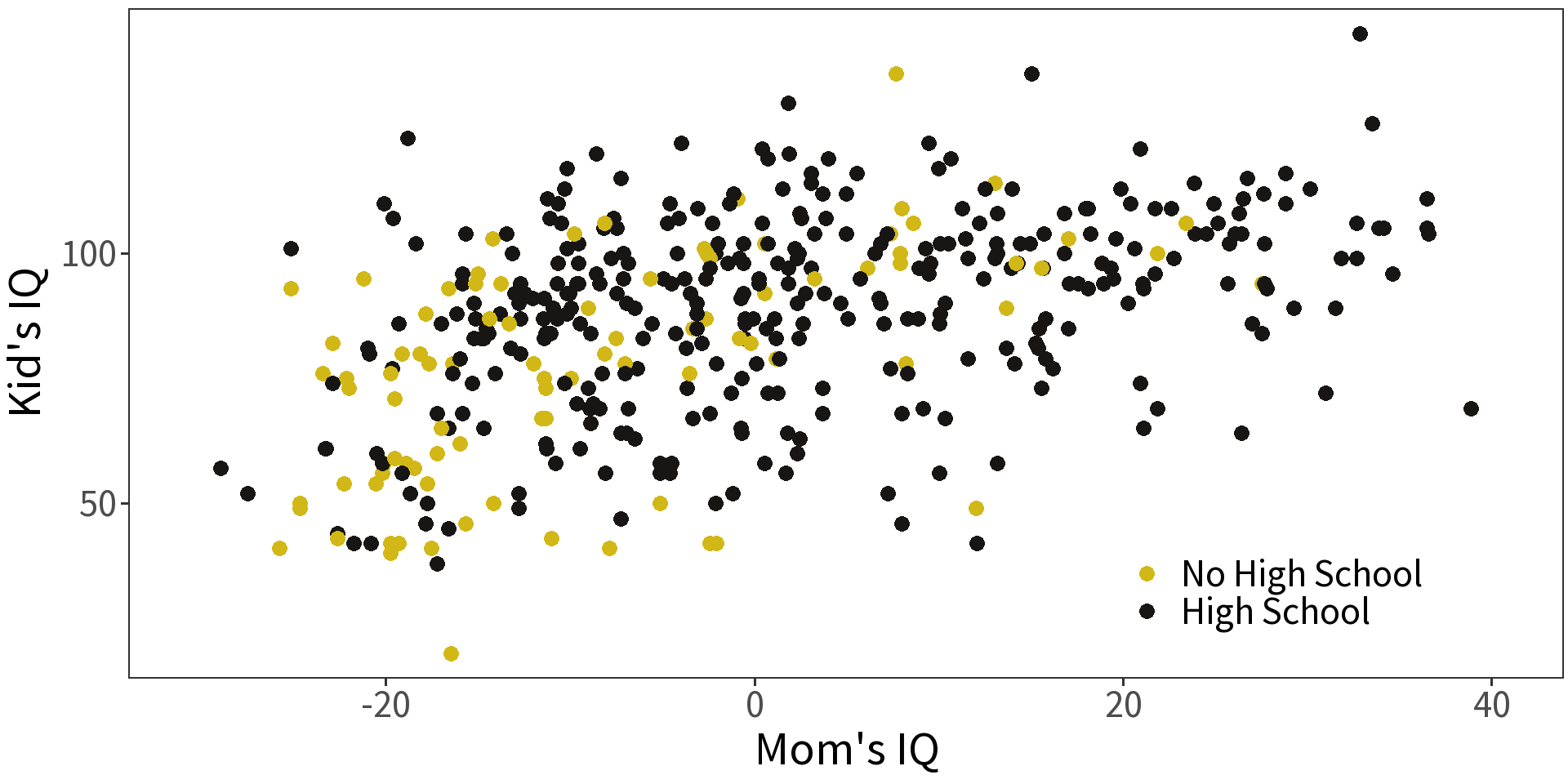
Question What if the relationship between child’s IQ and mother’s IQ depends on the mother’s educational attainment?

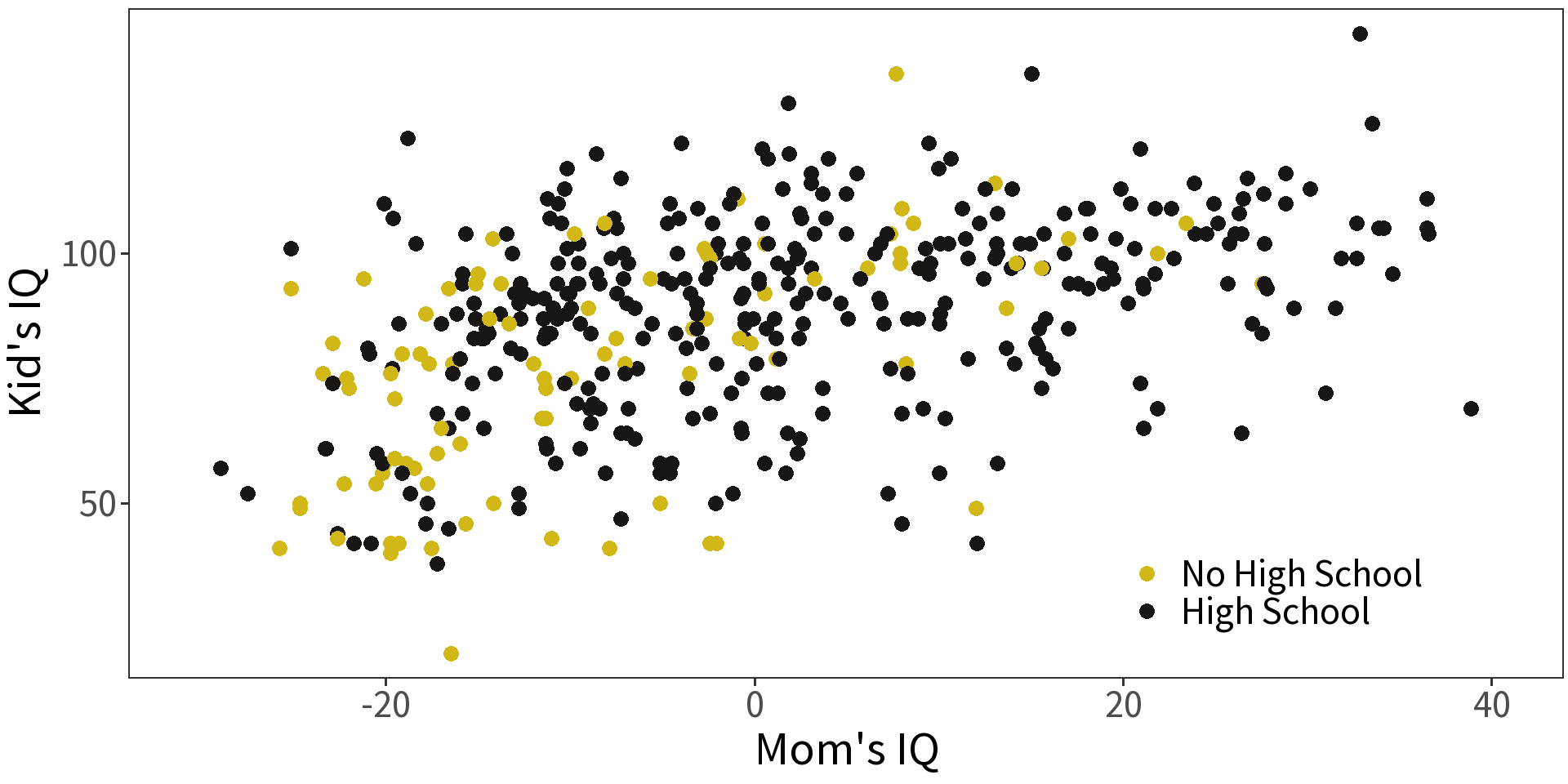
Simple formula becomes:

\[y_i = (\beta_0 + \gamma D) + (\beta_1x_1 + \omega D x_1) + \epsilon_i\]

With
- \(\gamma\) giving the change in \(\beta_0\) and
- \(\omega\) giving the change in \(\beta_1\).

That’s a change in intercept and a change in slope!

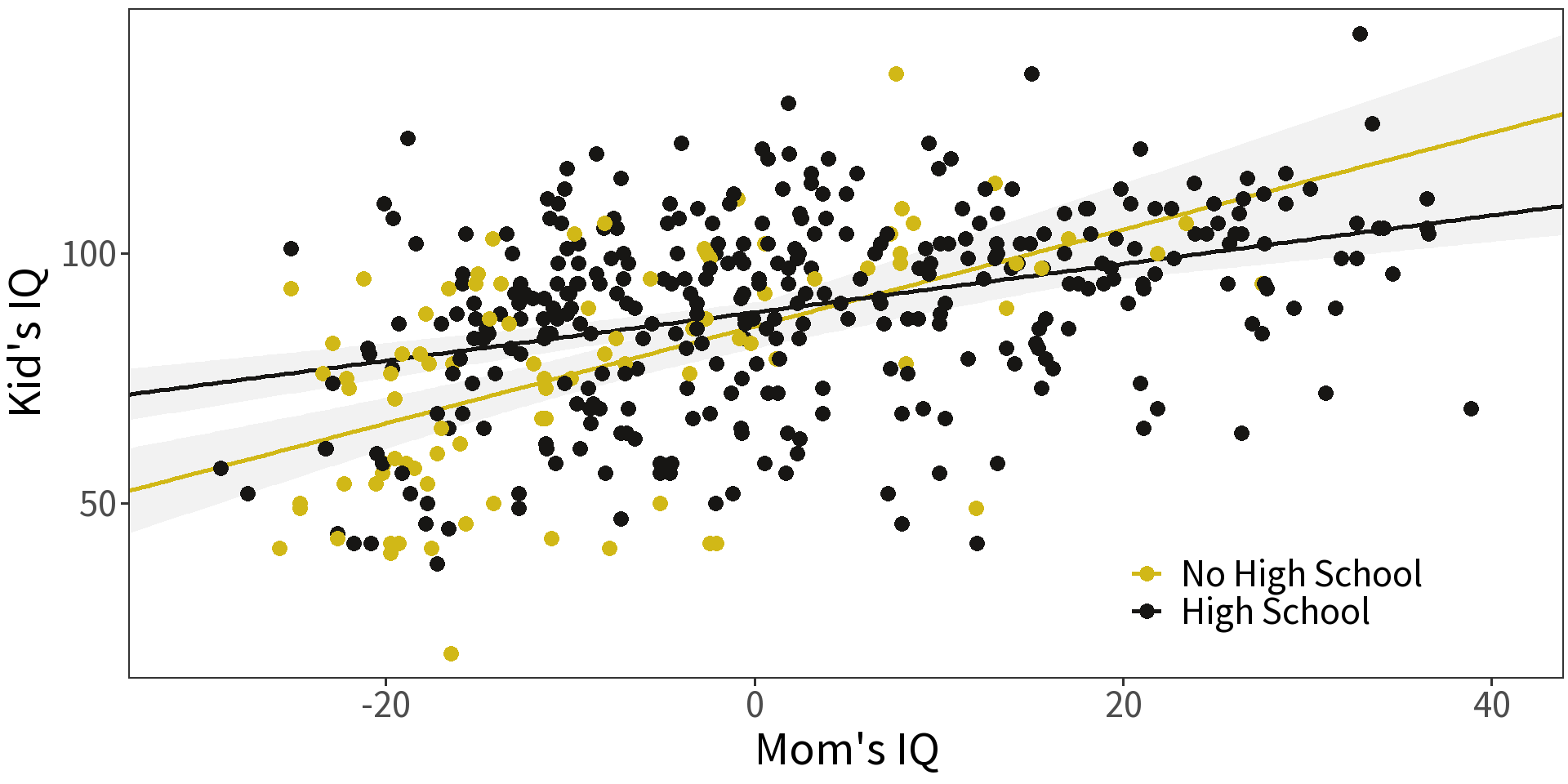
term	estimate	std.error	t.statistic	p.value
Additive Model
(Intercept)	86.797	0.877	98.993	0.000
Mom's IQ	0.610	0.059	10.423	0.000
Interactive Model
(Intercept)	85.407	2.218	38.502	0.000
Mom's IQ	0.969	0.148	6.531	0.000
High School	2.841	2.427	1.171	0.242
Mom's IQ x HS	-0.484	0.162	-2.985	0.003

Polynomial transformations for non-linearity

Simple Linear Model: \(y_{i} = \beta_{0} + \beta_{1}X + \epsilon_{i}\)
\(R^2 = 0.3088\)

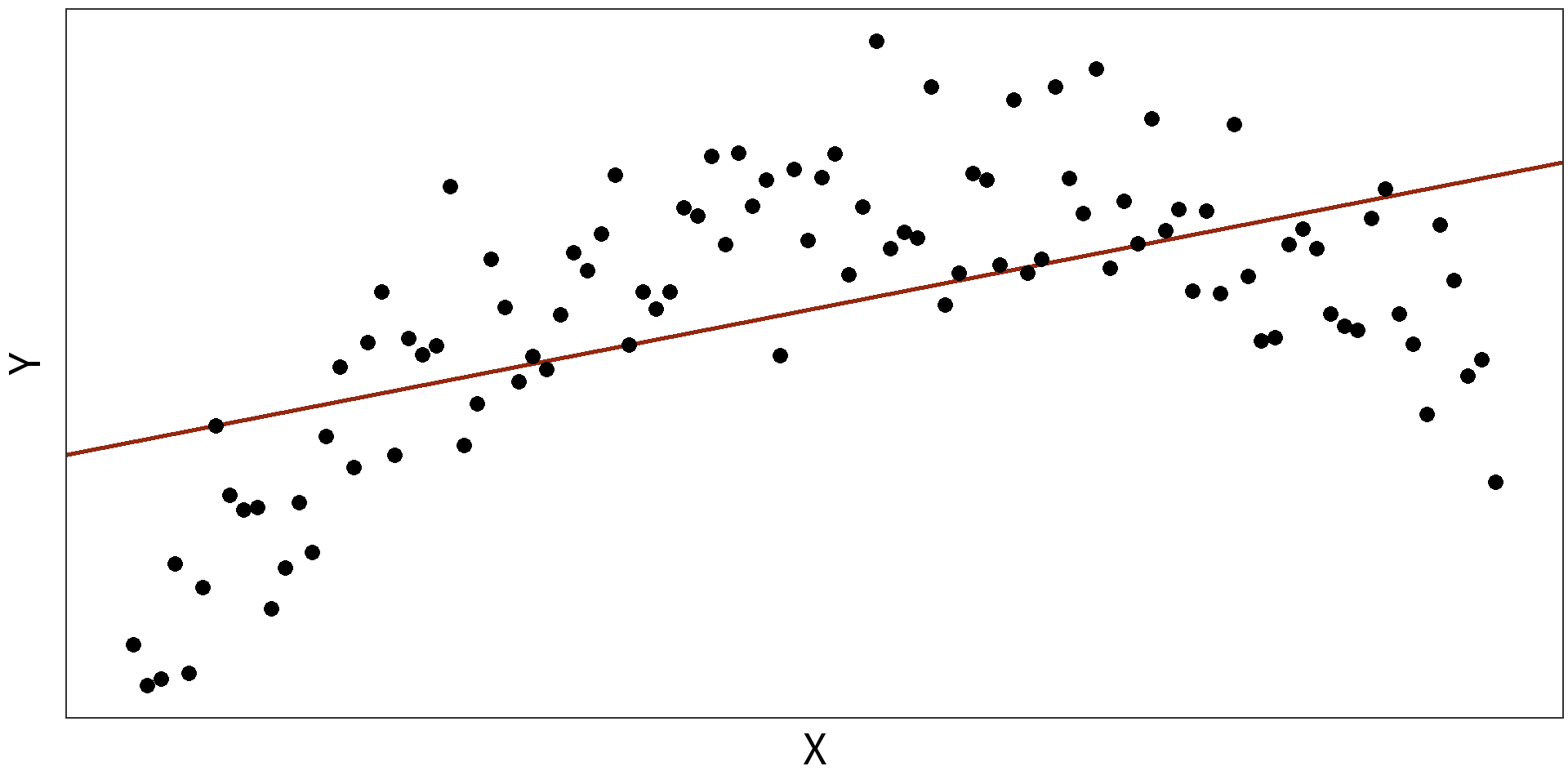
Quadratic Model: \(y_{i} = \beta_{0} + \beta_{1}X + \beta_{2}X^{2} + \epsilon_{i}\)
\(R^2=0.7636\)

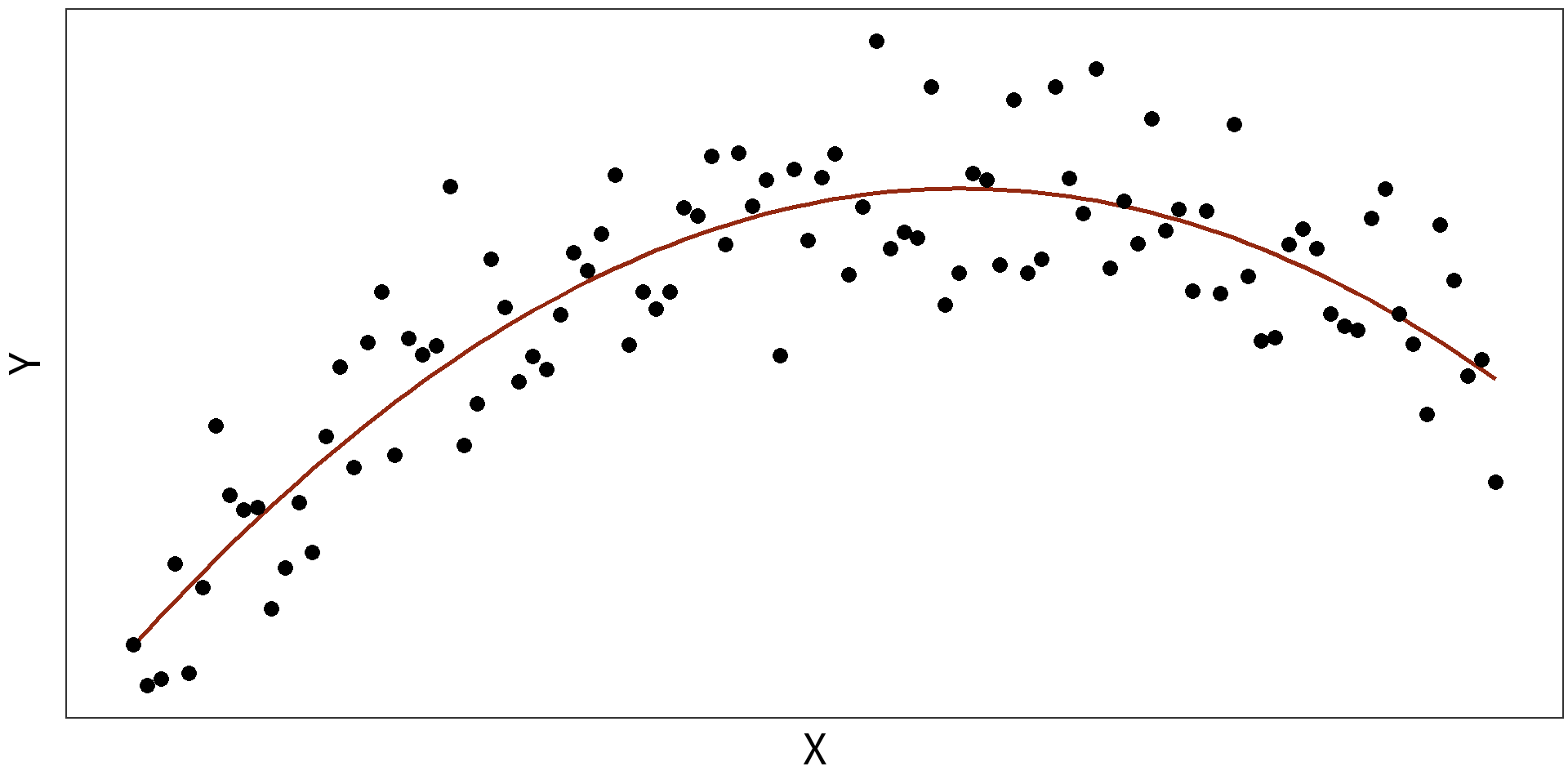
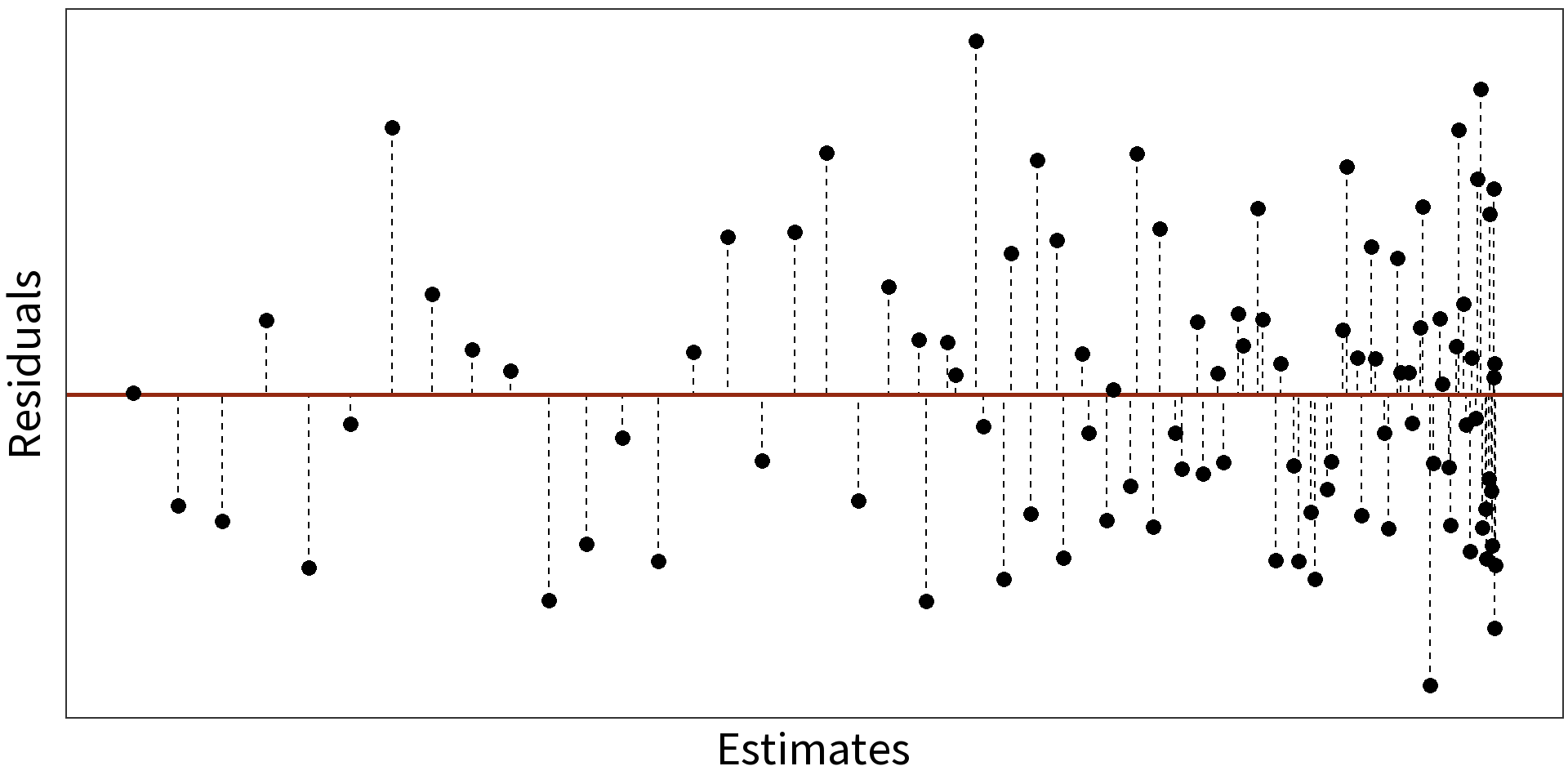
Log transformations

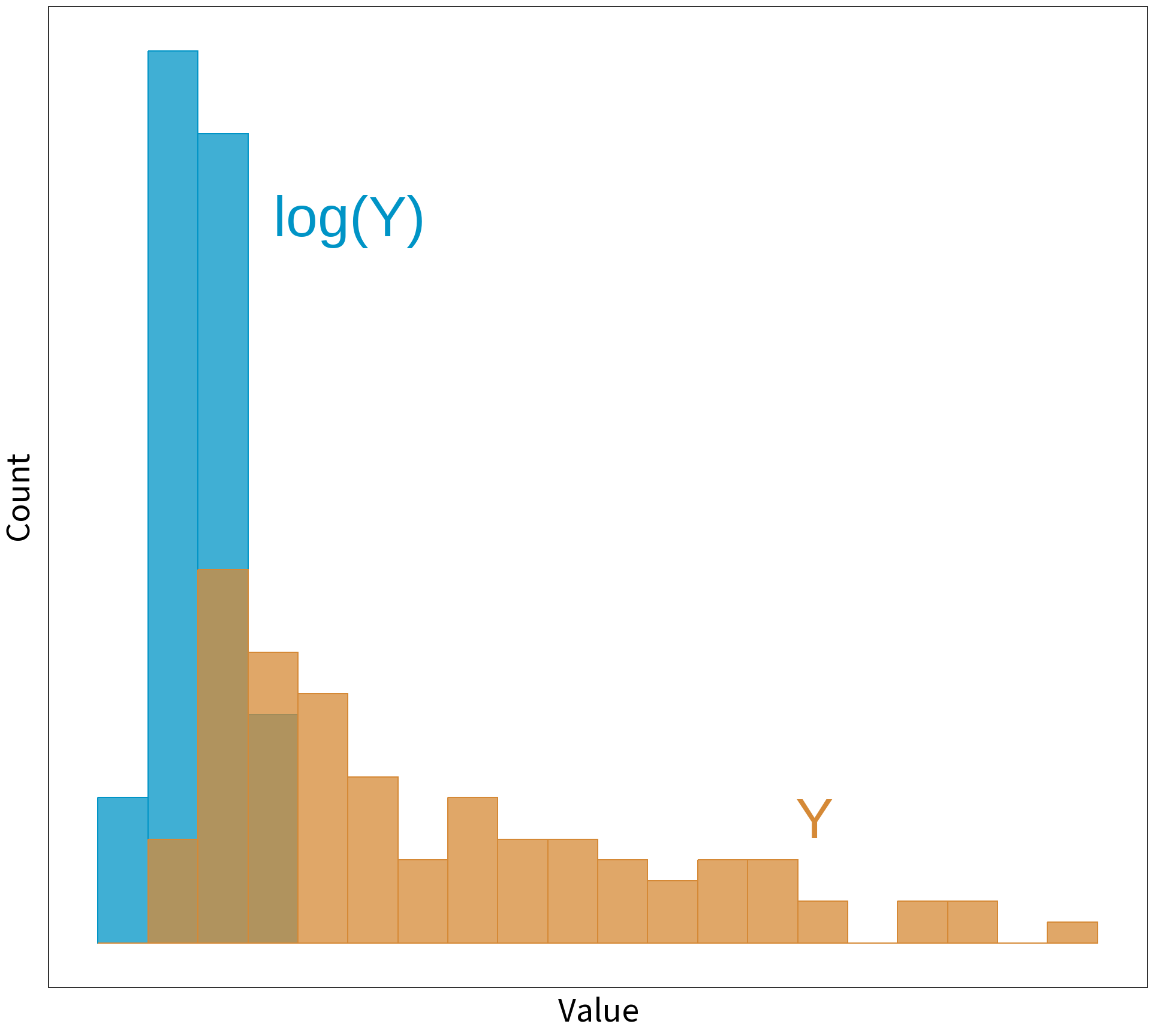
Logging a skewed variable normalizes it.

This is the inverse of exponentiation:

\[Y = log(exp(Y))\]

May be applied to \(X\) and \(Y\).

Question: but, whyyyyyy???

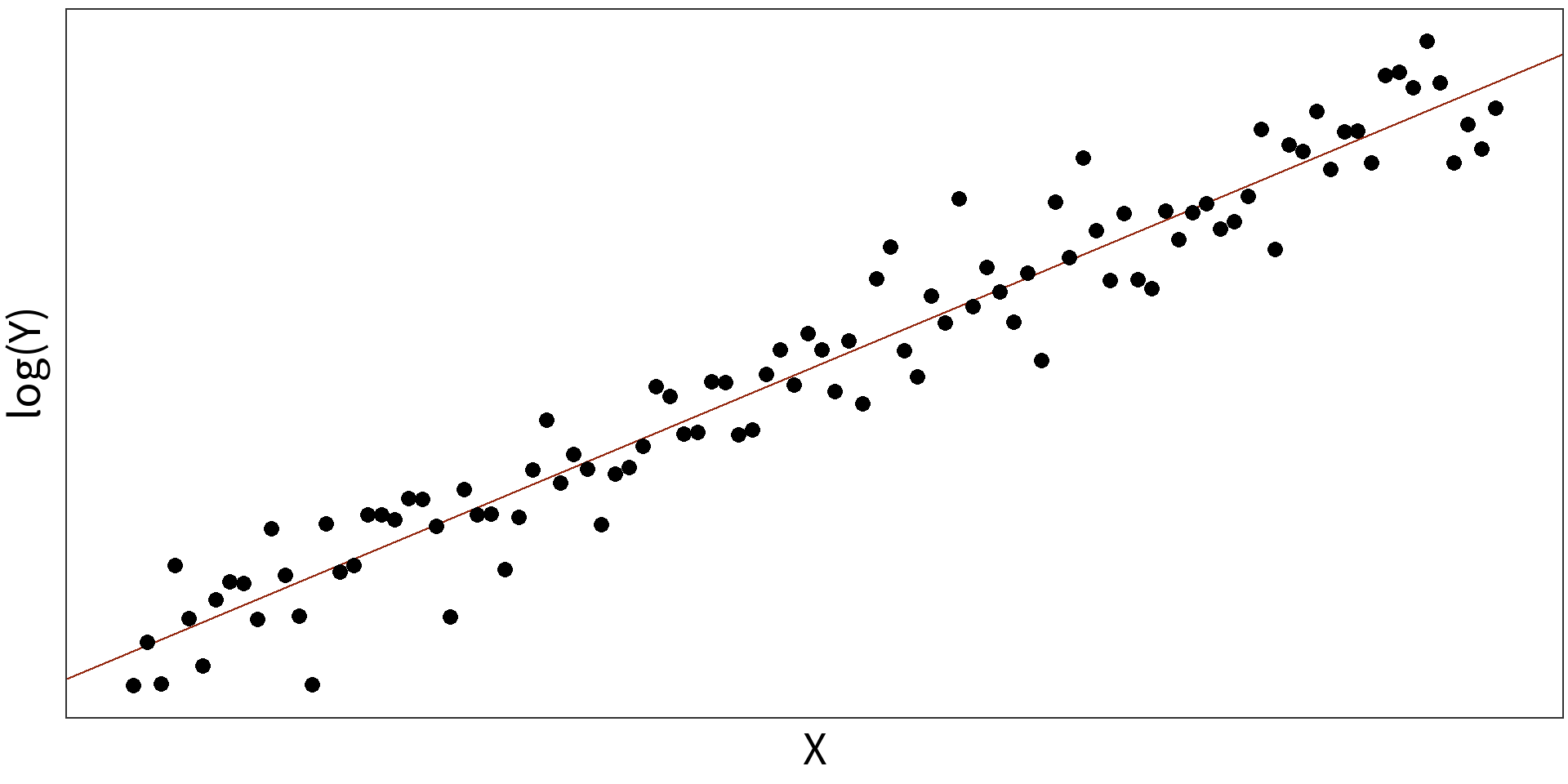
Log transformations for non-linearity

Simple Linear Model: \(y_{i} = \beta_{0} + \beta_{1}X + \epsilon_{i}\)
\(R^2 = 0.8325\)

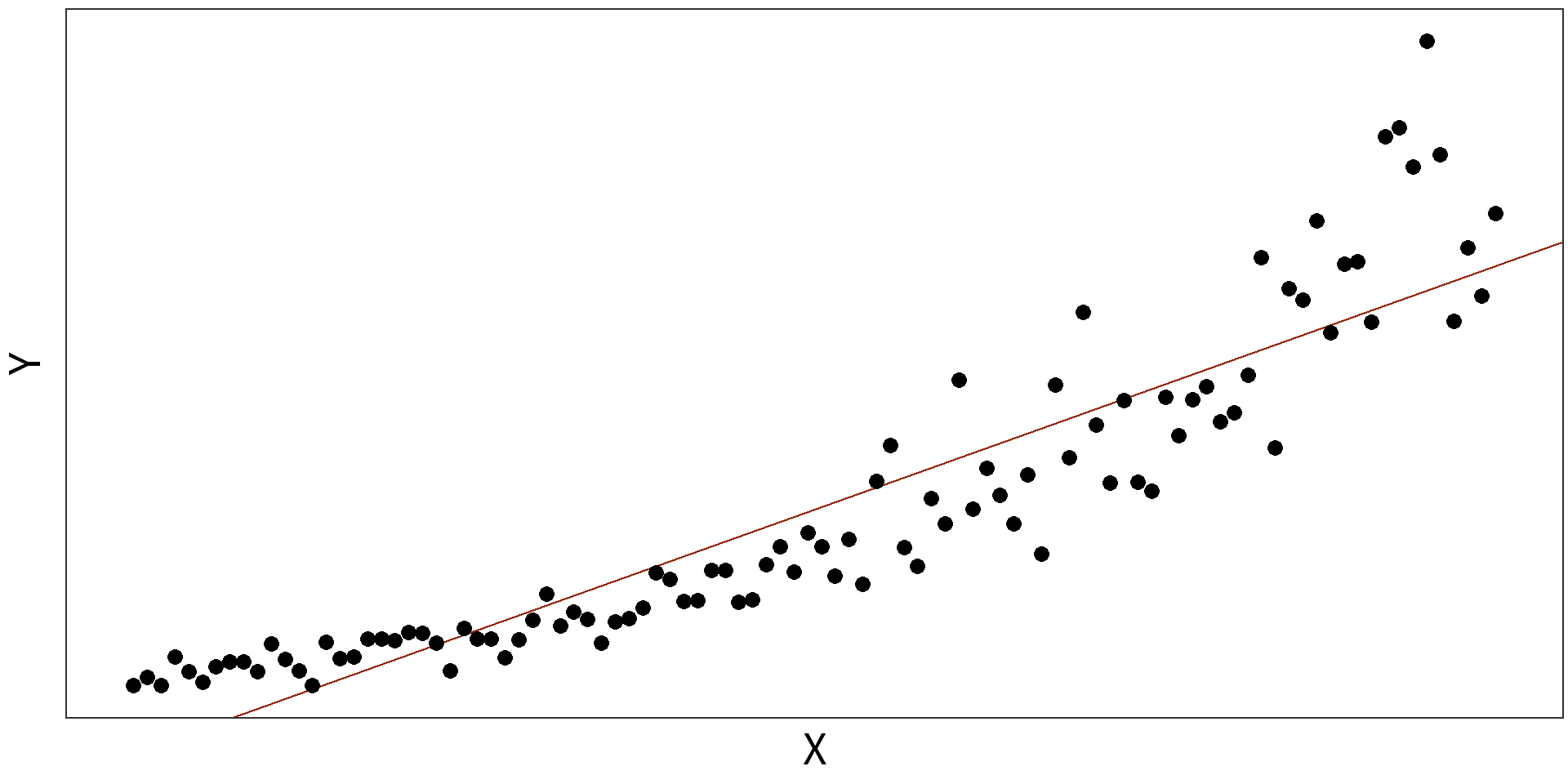
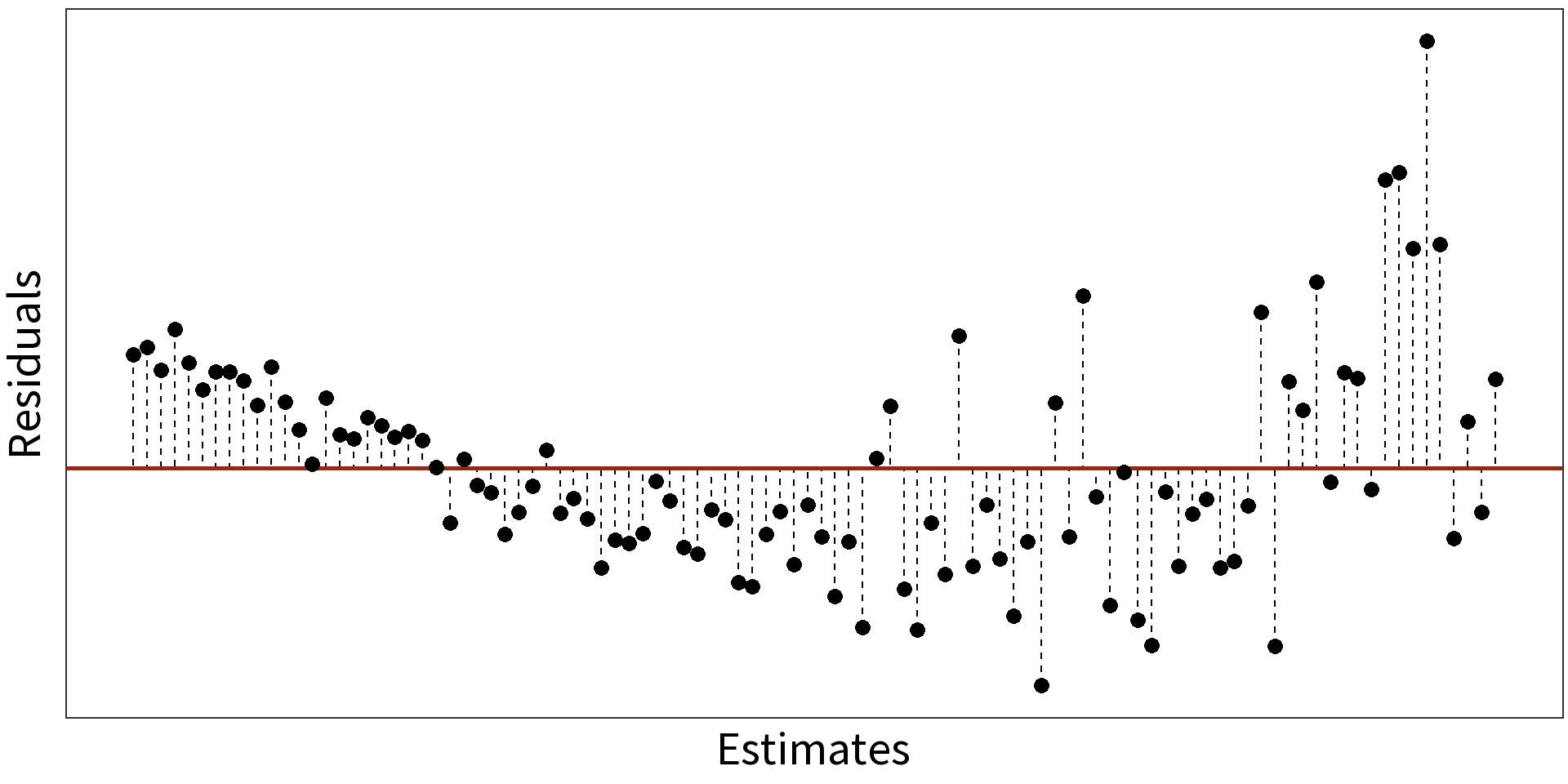
Log Linear Model: \(log(y_{i}) = \beta_{0} + \beta_{1}X + \epsilon_{i}\)
\(R^2 = 0.9407\)

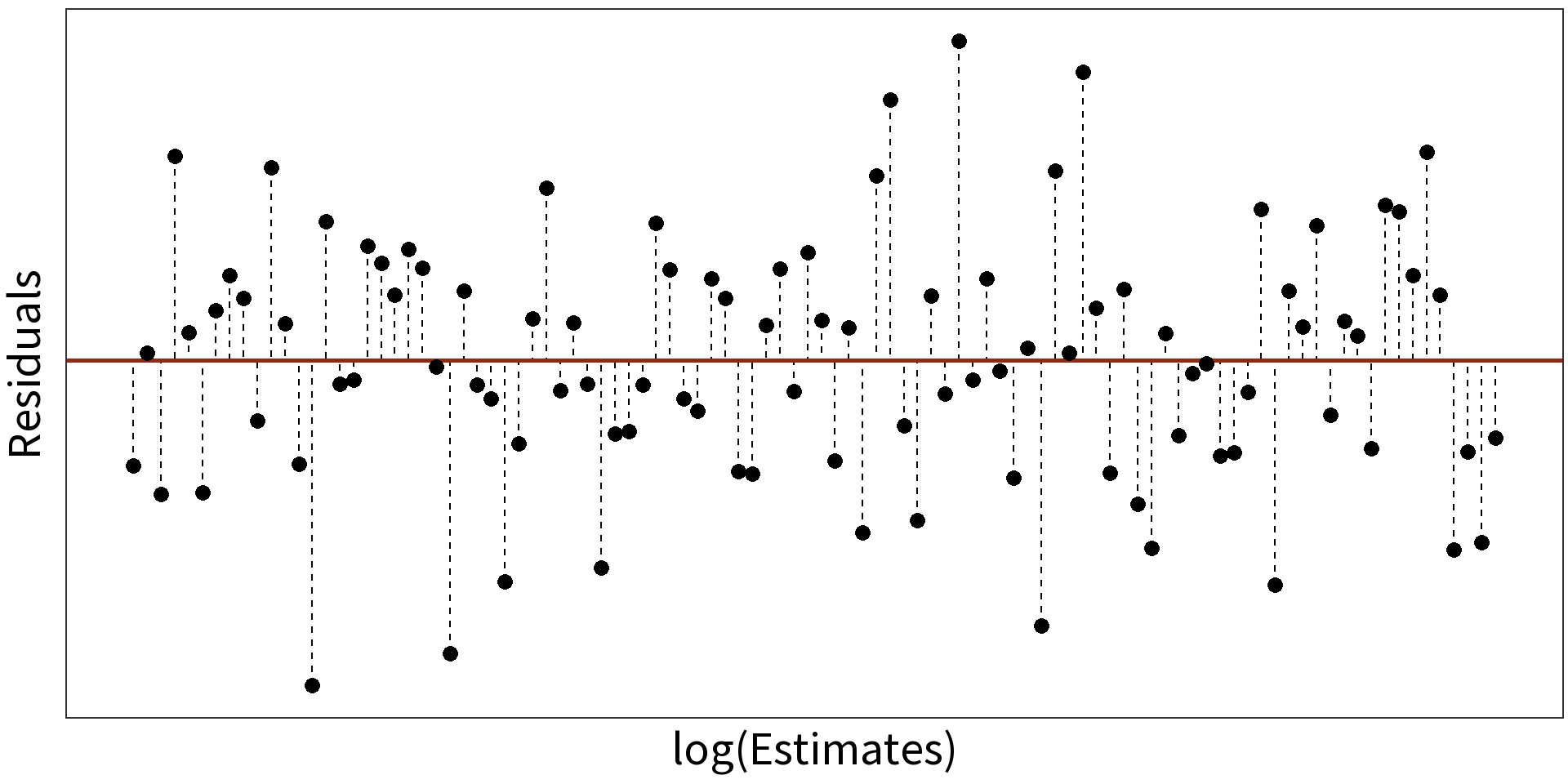
⚠️ Careful!

Have to take care how we interpret log-models!

\(\beta_1\) means…

Linear Model
\(y_{i} = \beta_{0} + \beta_{1}X + \epsilon_{i}\)
Increase in Y for one unit increase in X.

Log-Linear Model
\(log(y_{i}) = \beta_{0} + \beta_{1}X + \epsilon_{i}\)
Percent increase in Y for one unit increase in X.

Linear-Log Model
\(y_{i} = \beta_{0} + \beta_{1}log(X) + \epsilon_{i}\)
Increase in Y for percent increase in X.

Log-Log Model
\(log(y_{i}) = \beta_{0} + \beta_{1}log(X) + \epsilon_{i}\)
Percent increase in Y for percent increase in X.