Lecture 02: Probability as a Model
2/20/23
📋 Lecture Outline
- Why statistics?
- 🧪 A simple experiment
- Some terminology
- 🎰 Random variables
- 🎲 Probability
- 📊 Probability Distribution
- Probability Distribution as a Model
- Probability Distribution as a Function
- Probability Mass Functions
- Probability Density Functions
- 🚗 Cars Model
- Brief Review
- A Simple Formula
- A Note About Complexity
Setup
Why statistics?




We want to understand something about a population.
We can never observe the entire population, so we draw a sample.
We then use a model to describe the sample.
By comparing that model to a null model, we can infer something about the population.
Here, we’re going to focus on statistical description, aka models.
🧪 A simple experiment
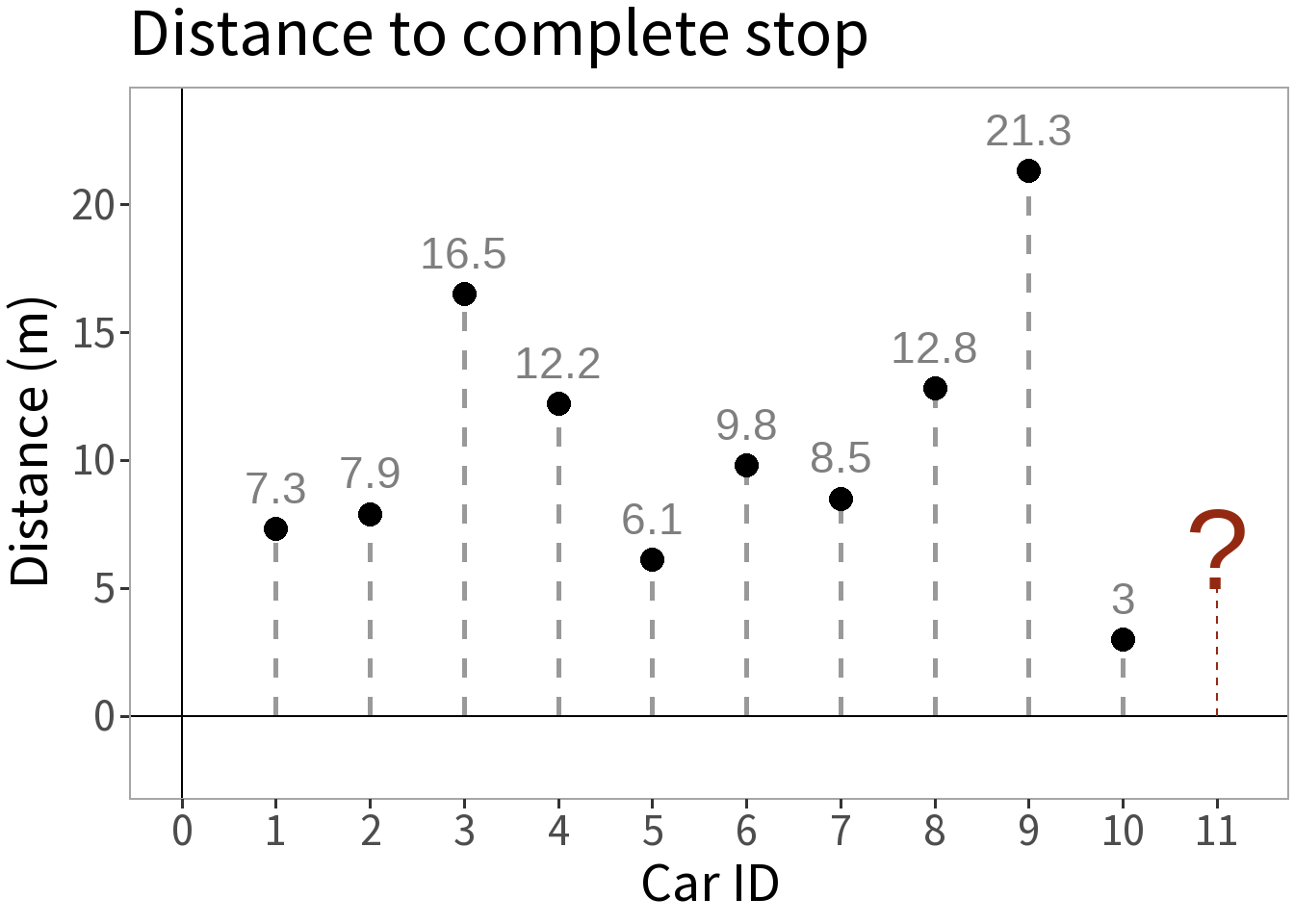
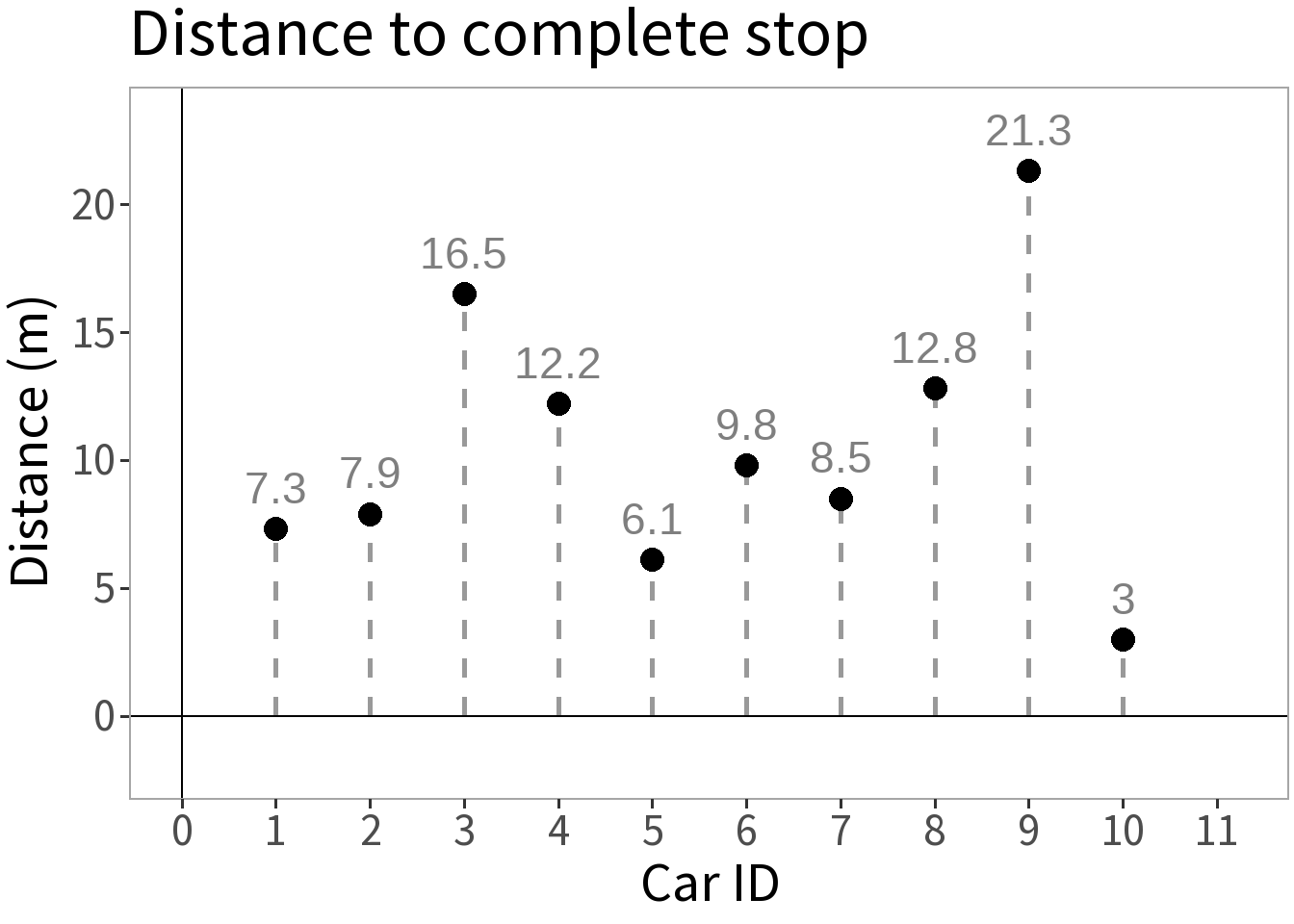
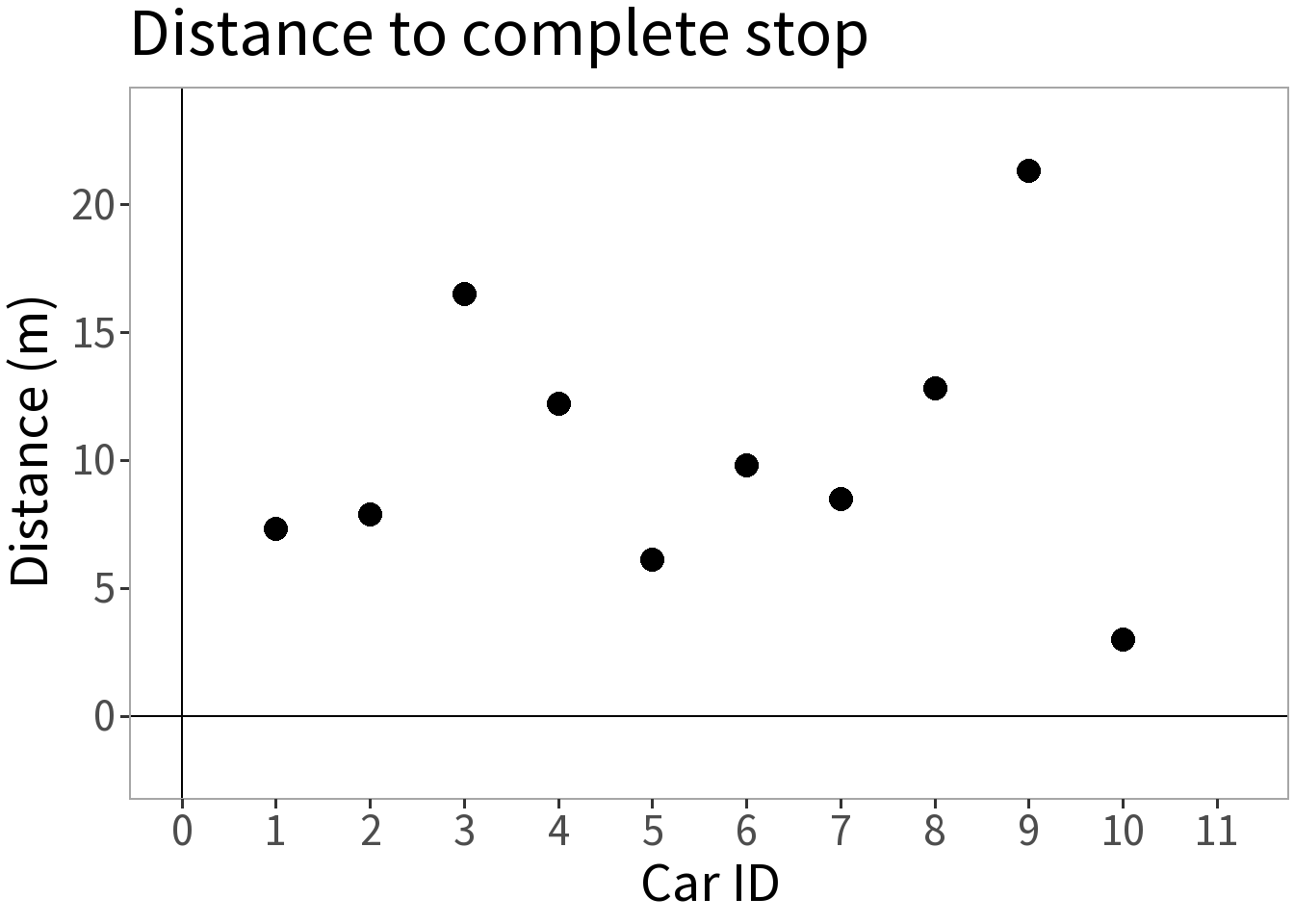
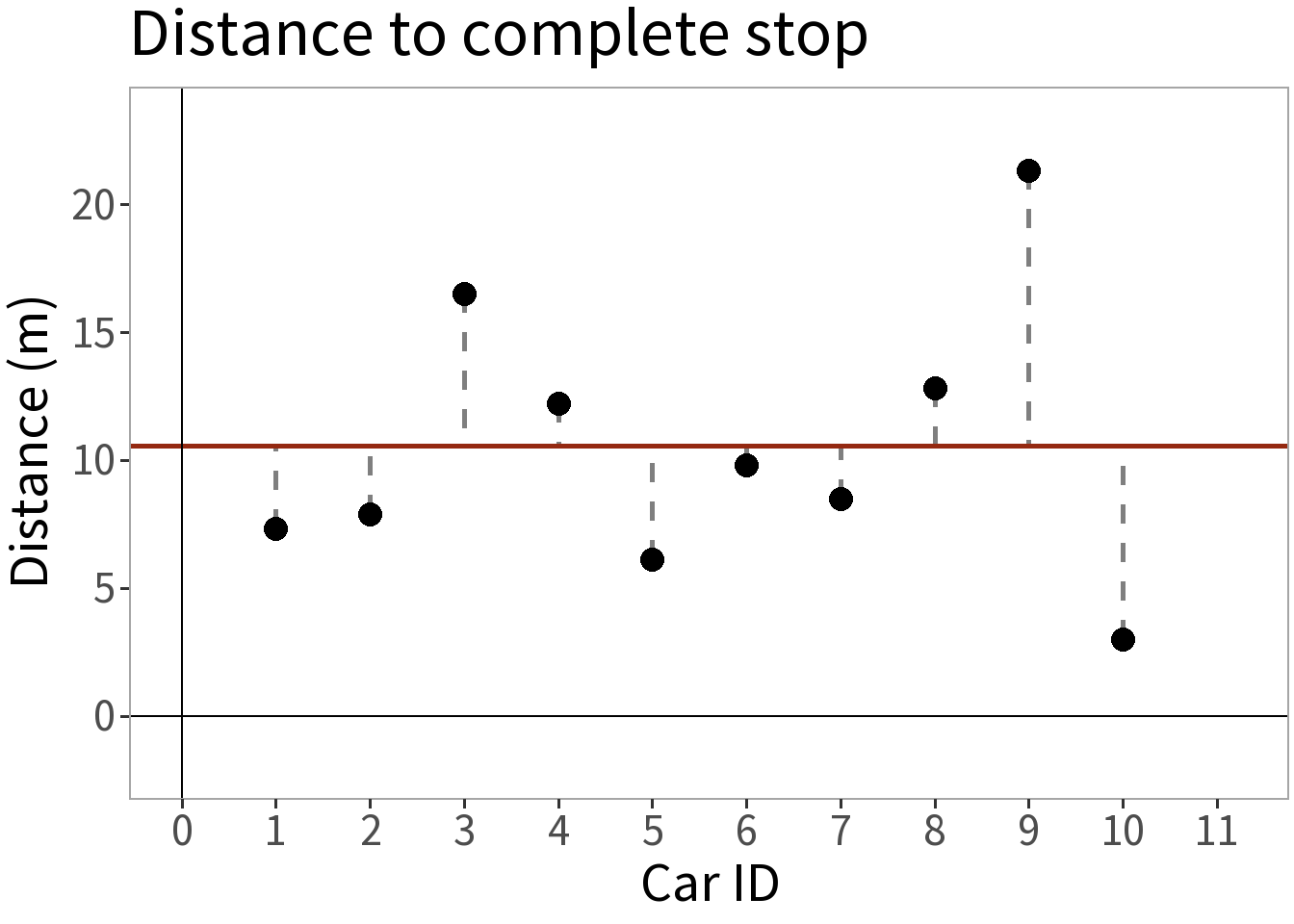
We take ten cars, send each down a track, have them brake at the same point, and measure the distance it takes them to stop.
Question: how far do you think it will take the next car to stop?
Question: what distance is the most probable?
But, how do we determine this?
Some terminology




🎰 Random Variables
Two types of random variable:
- Discrete random variables often take only integer (non-decimal) values.
- Examples: number of heads in 10 tosses of a fair coin, number of victims of the Thanos snap, number of projectile points in a stratigraphic level, number of archaeological sites in a watershed.
- Continuous random variables take real (decimal) values.
- Examples: cost in property damage of a superhero fight, kilocalories per kilogram, kilocalories per hour, ratio of isotopes
- Note: for continuous random variables, the sample space is infinite!
- Examples: cost in property damage of a superhero fight, kilocalories per kilogram, kilocalories per hour, ratio of isotopes
Probability Distributions
🎲 Probability
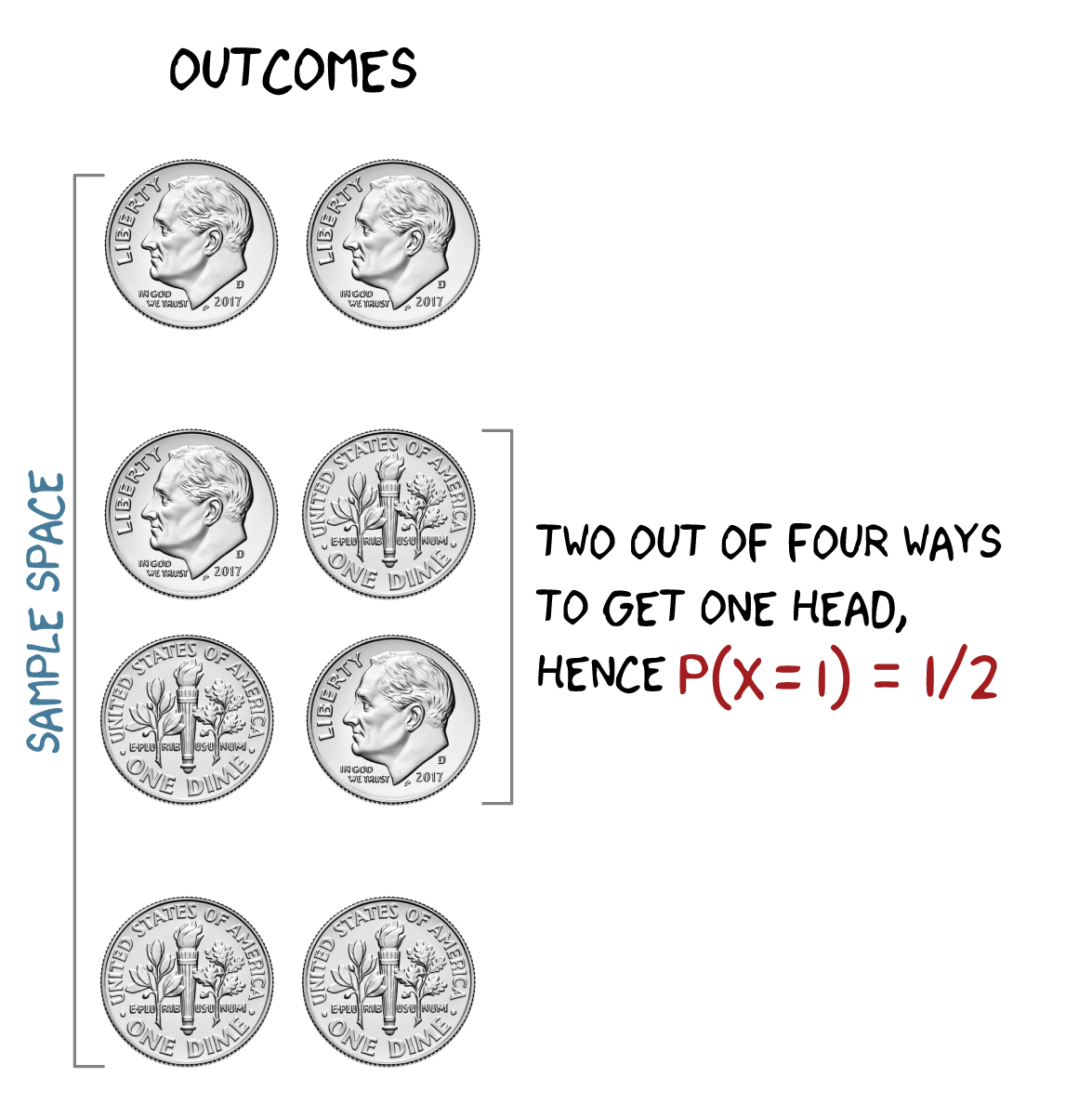
Let \(X\) be the number of heads in two tosses of a fair coin. What is the probability that \(X=1\)?
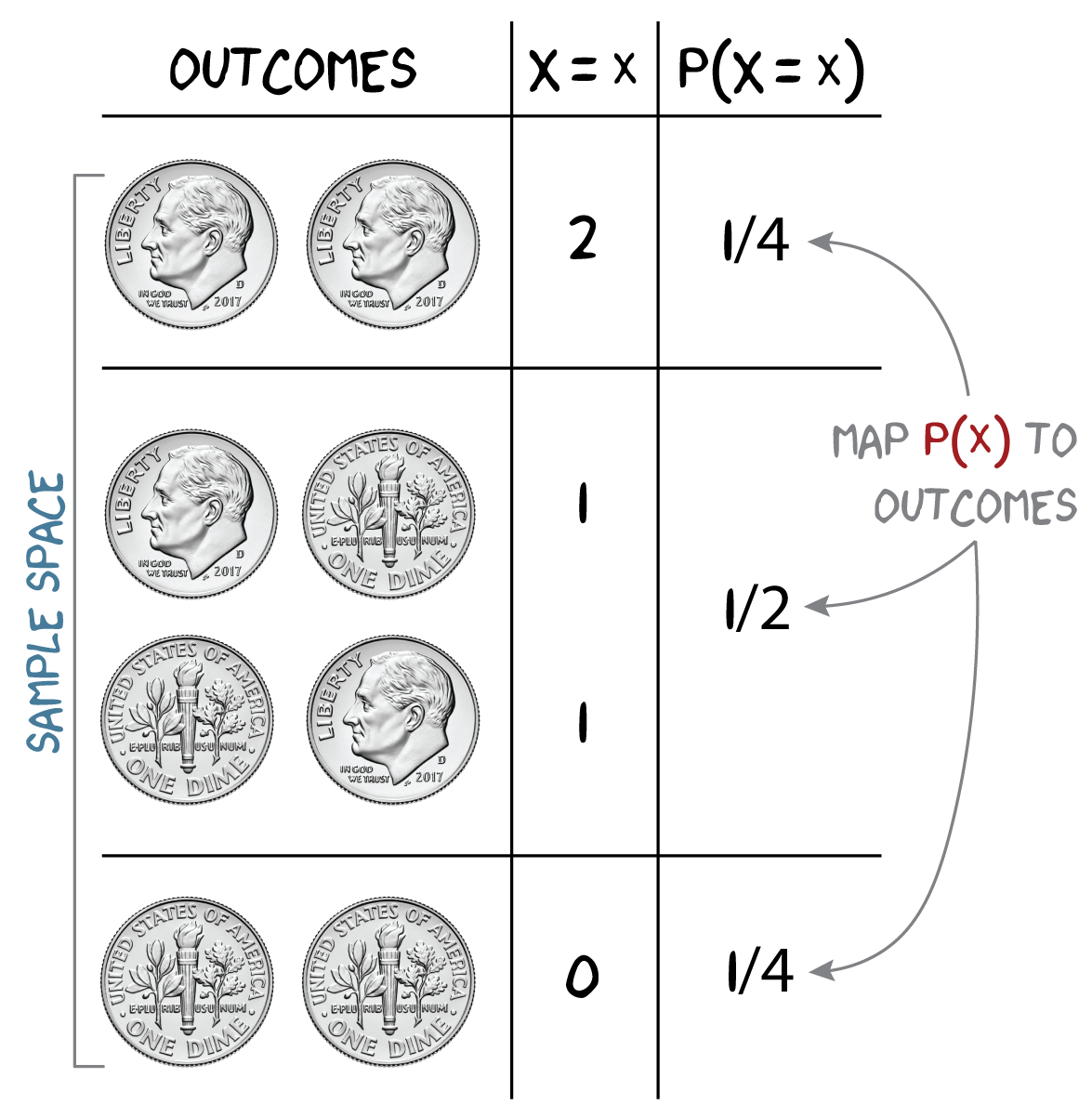
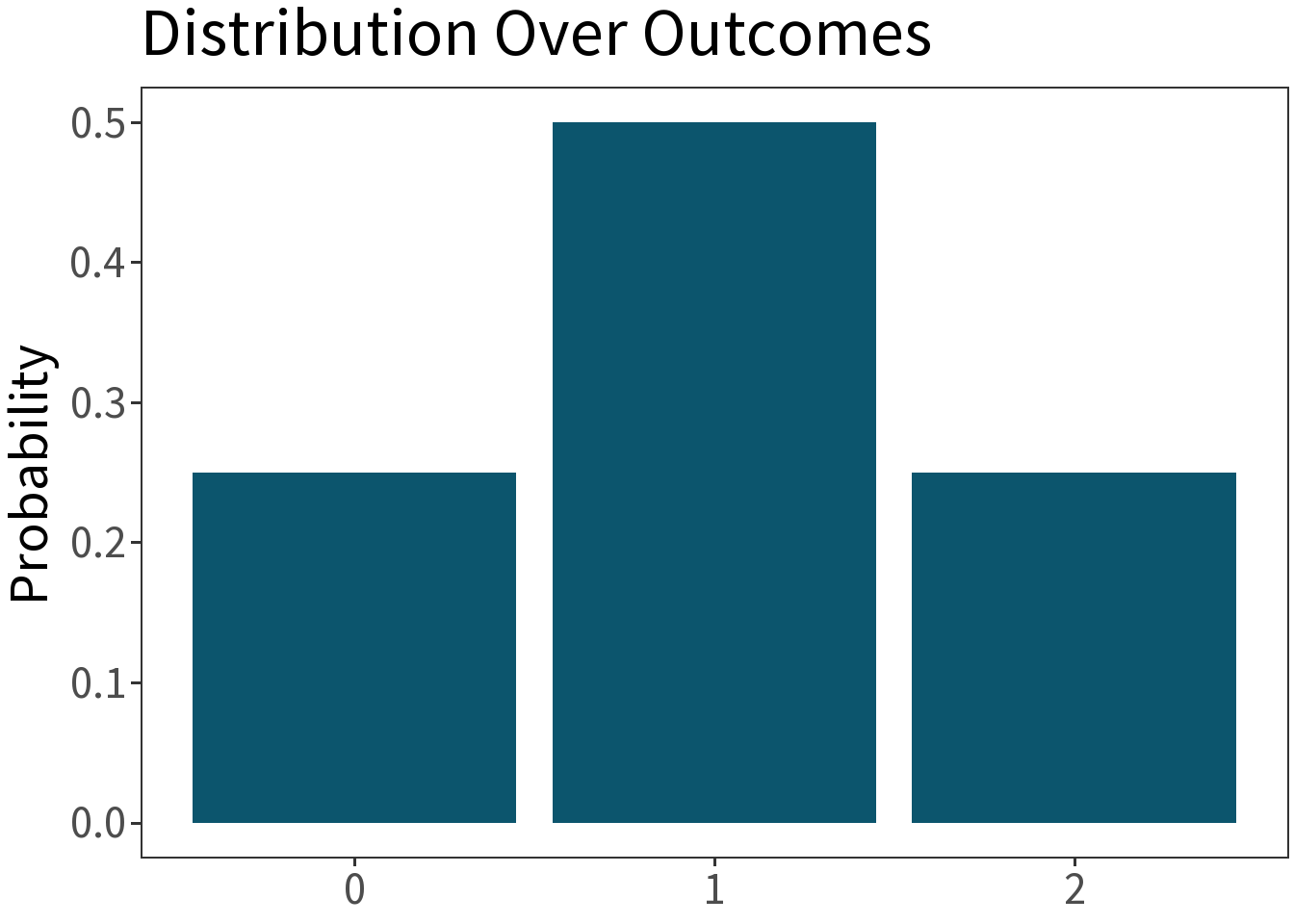
Probability Distribution as a Model
Has two components:
Central-tendency or “first moment”
- Population mean (\(\mu\)). Gives the expected value of an experiment, \(E[X] = \mu\).
- Sample mean (\(\bar{x}\)). Estimate of \(\mu\) based on a sample from \(X\) of size \(n\).
Dispersion or “second moment”
- Population variance (\(\sigma^2\)). The expected value of the squared difference from the mean.
- Sample variance (\(s^2\)). Estimate of \(\sigma^2\) based on a sample from \(X\) of size \(n\).
- Standard deviation (\(\sigma\)) or \(s\) is the square root of the variance.
Probability Distribution as a Function
These can be defined using precise mathematical functions:
A probability mass function (PMF) for discrete random variables.
- Examples: Bernoulli, Binomial, Negative Binomial, Poisson
- Straightforward probability interpretation.
A probability density function (PDF) for continuous random variables.
- Examples: Normal, Chi-squared, Student’s t, and F
- Harder to interpret probability:
- What is the probability that a car takes 10.317 m to stop? What about 10.31742 m?
- Better to consider probability across an interval.
- What is the probability that a car takes 10.317 m to stop? What about 10.31742 m?
- Requires that the function integrate to one (probability is the area under the curve).
Probability Mass Functions (PMF)
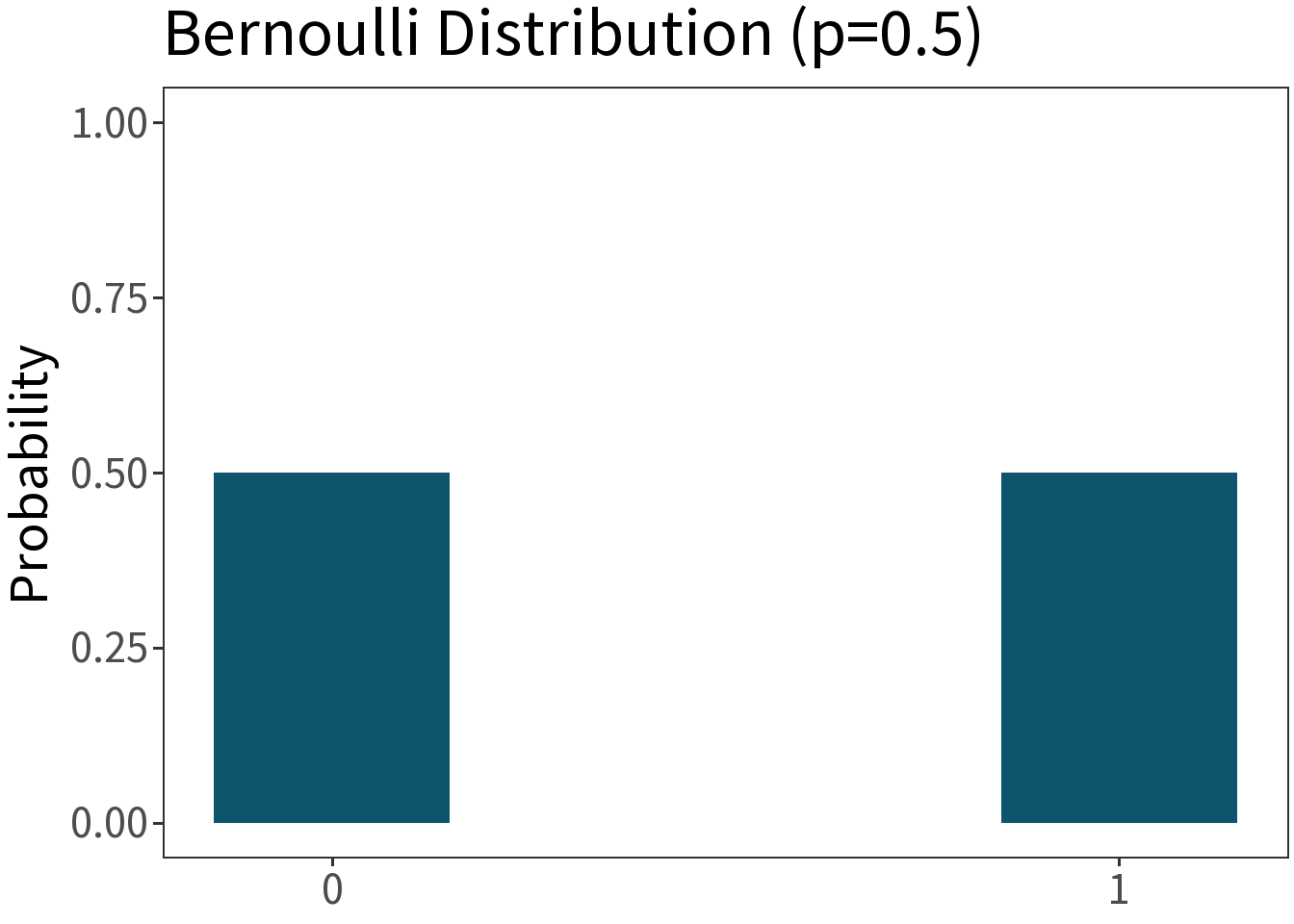
Bernoulli
Df. distribution of a binary random variable (“Bernoulli trial”) with two possible values, 1 (success) and 0 (failure), with \(p\) being the probability of success. E.g., a single coin flip.
\[f(x,p) = p^{x}(1-p)^{1-x}\]
Mean: \(p\)
Variance: \(p(1-p)\)
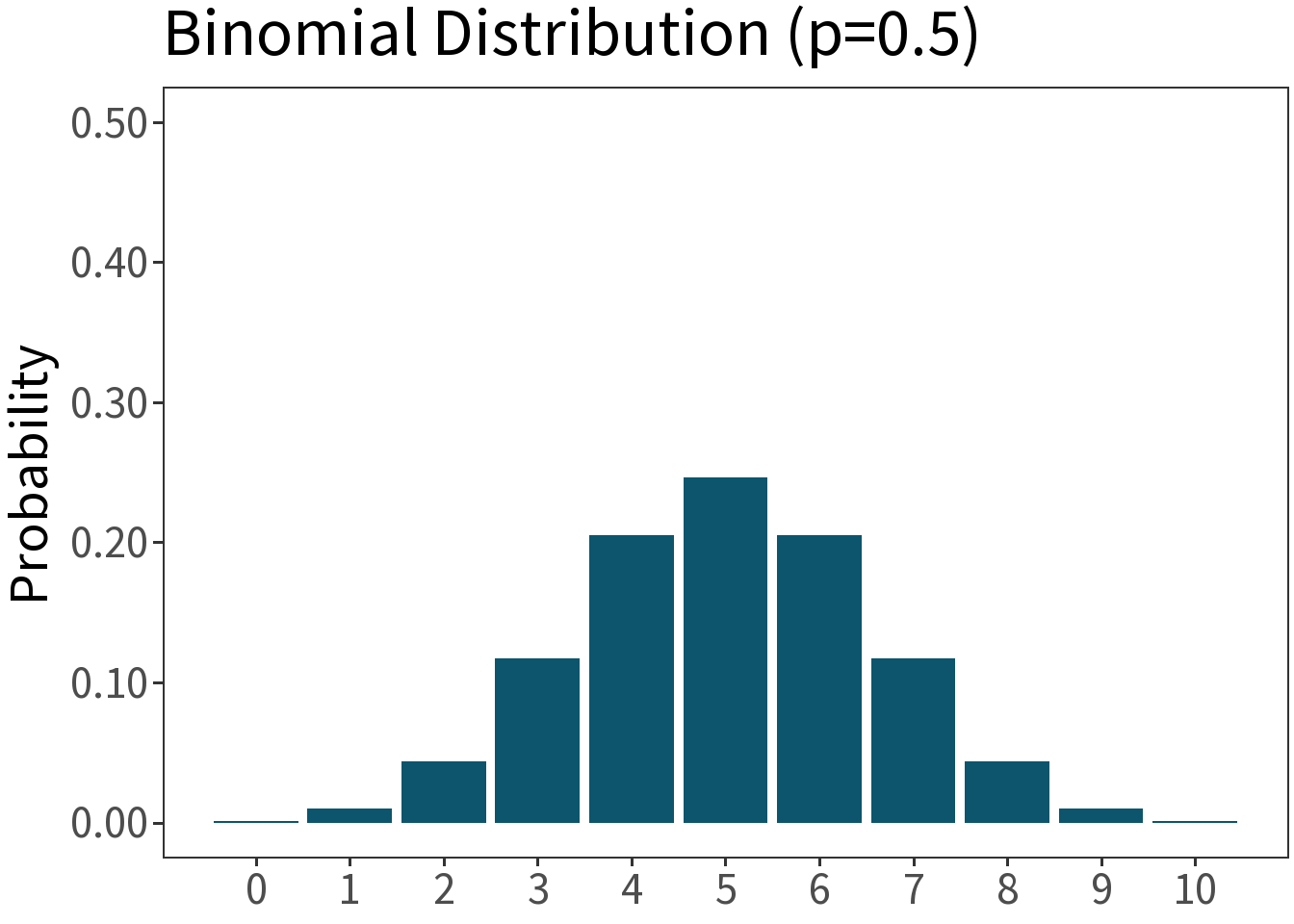
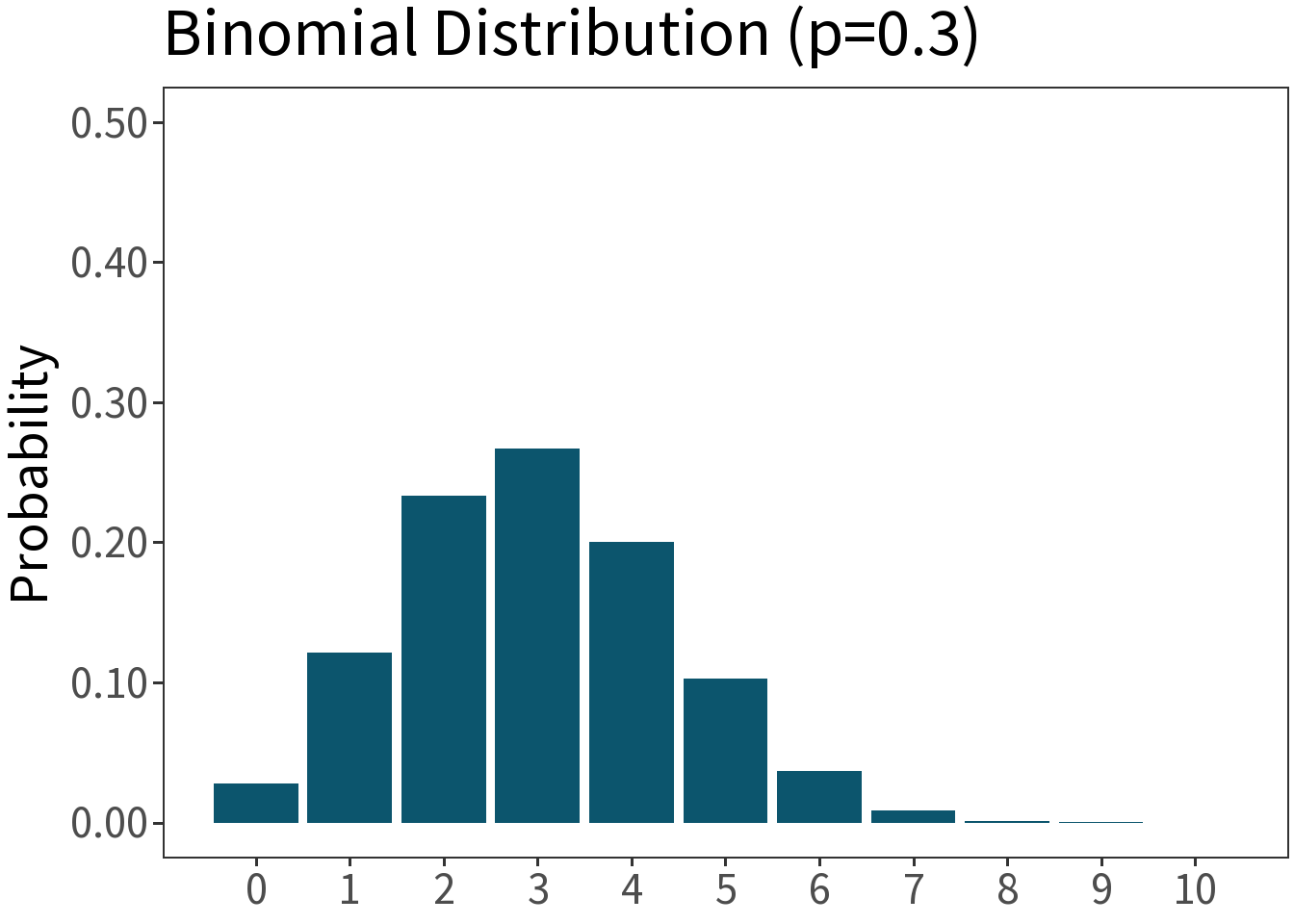
Binomial
Df. distribution of a random variable whose value is equal to the number of successes in \(n\) independent Bernoulli trials. E.g., number of heads in ten coin flips.
\[f(x,p,n) = \binom{n}{x}p^{x}(1-p)^{1-x}\]
Mean: \(np\)
Variance: \(np(1-p)\)
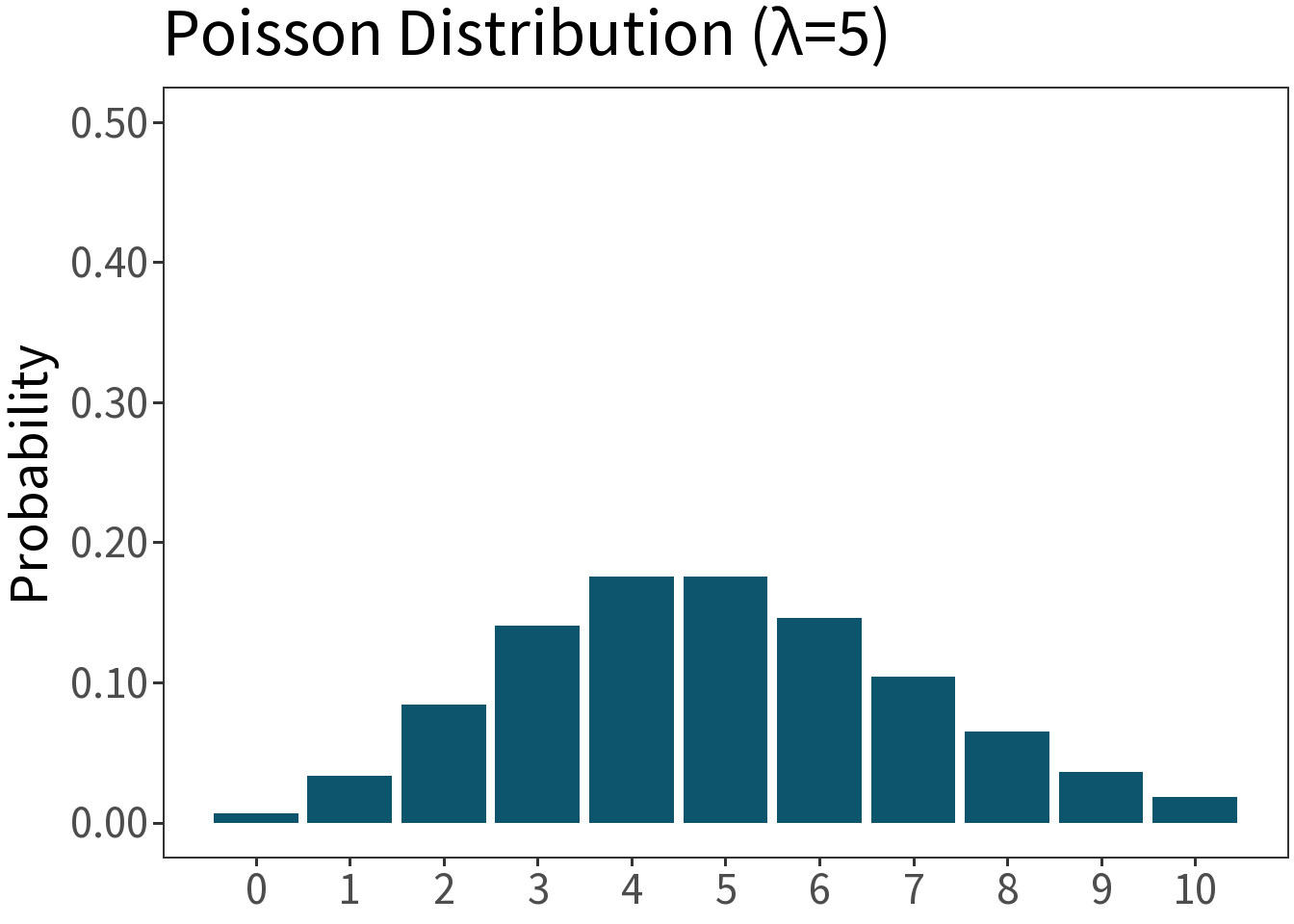
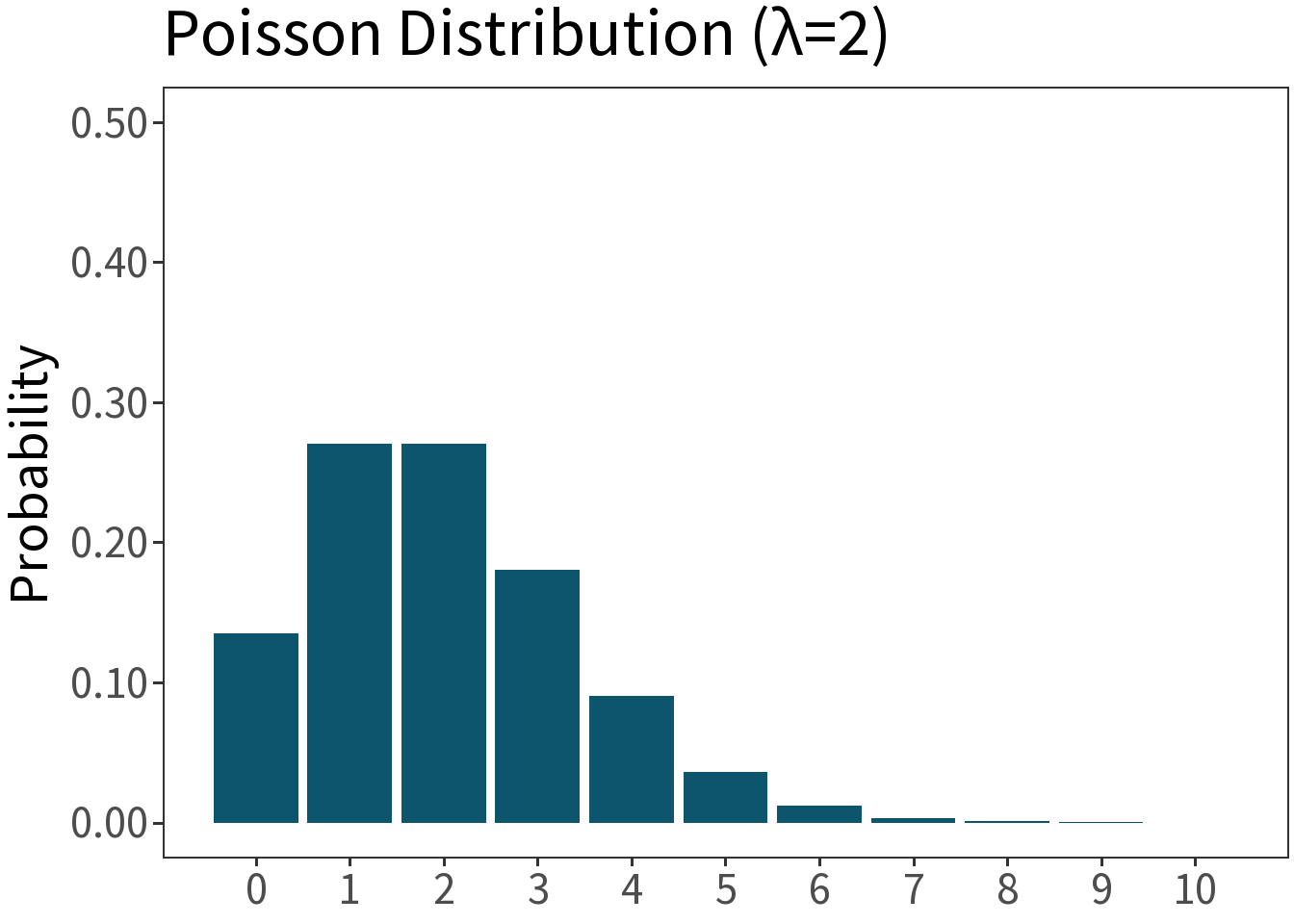
Poisson
Df. distribution of a random variable whose value is equal to the number of events occurring in a fixed interval of time or space. E.g., number of orcs passing through the Black Gates in an hour.
\[f(x,\lambda) = \frac{\lambda^{x}e^{-\lambda}}{x!}\]
Mean: \(\lambda\)
Variance: \(\lambda\)
Probability Density Functions (PDF)
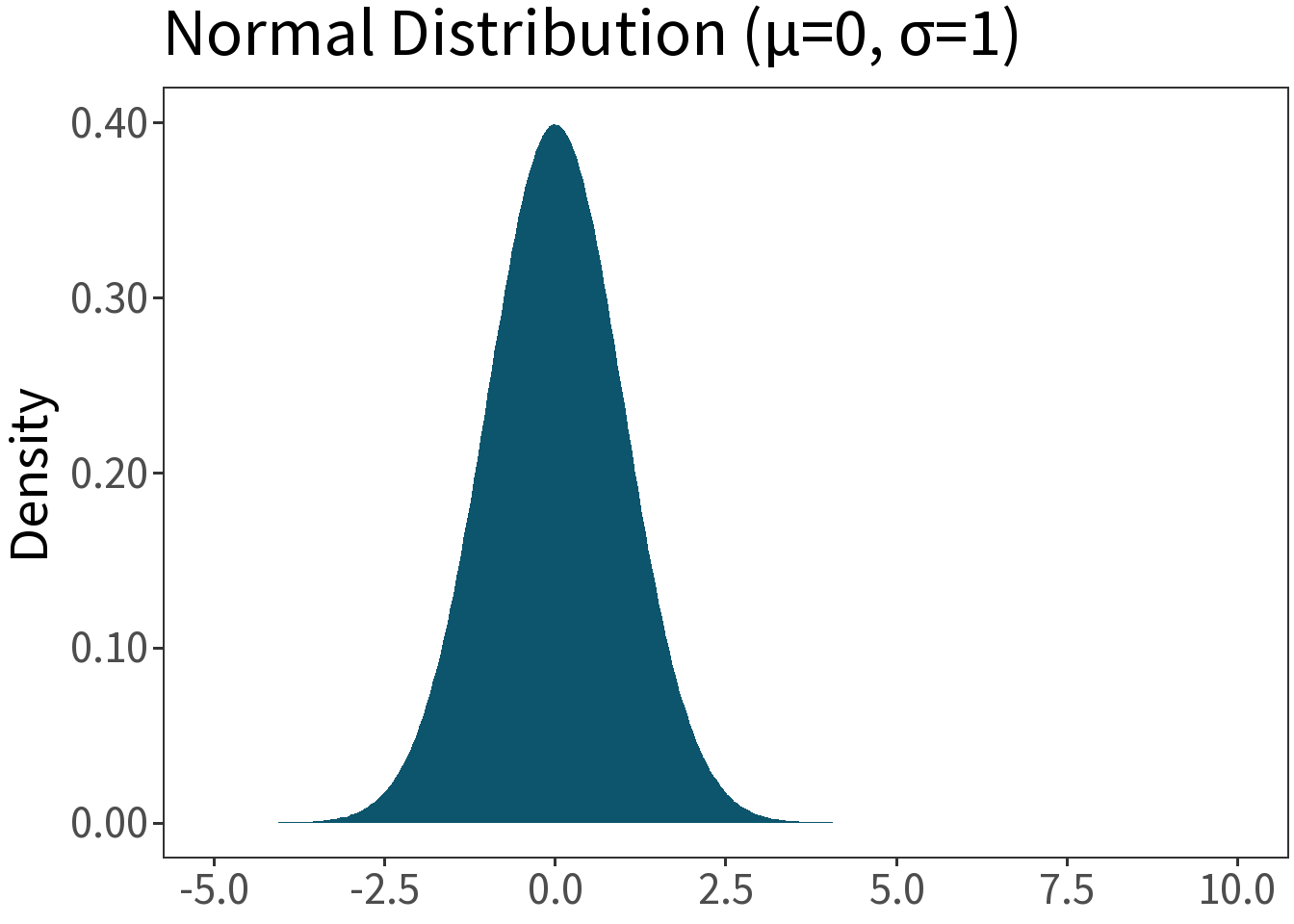
Normal (Gaussian)
Df. distribution of a continuous random variable that is symmetric from positive to negative infinity. E.g., the height of actors who auditioned for the role of Aragorn.
\[f(x,\mu,\sigma) = \frac{1}{\sqrt{2\pi\sigma^2}}\;exp\left[-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2\right]\]
Mean: \(\mu\)
Variance: \(\sigma^2\)
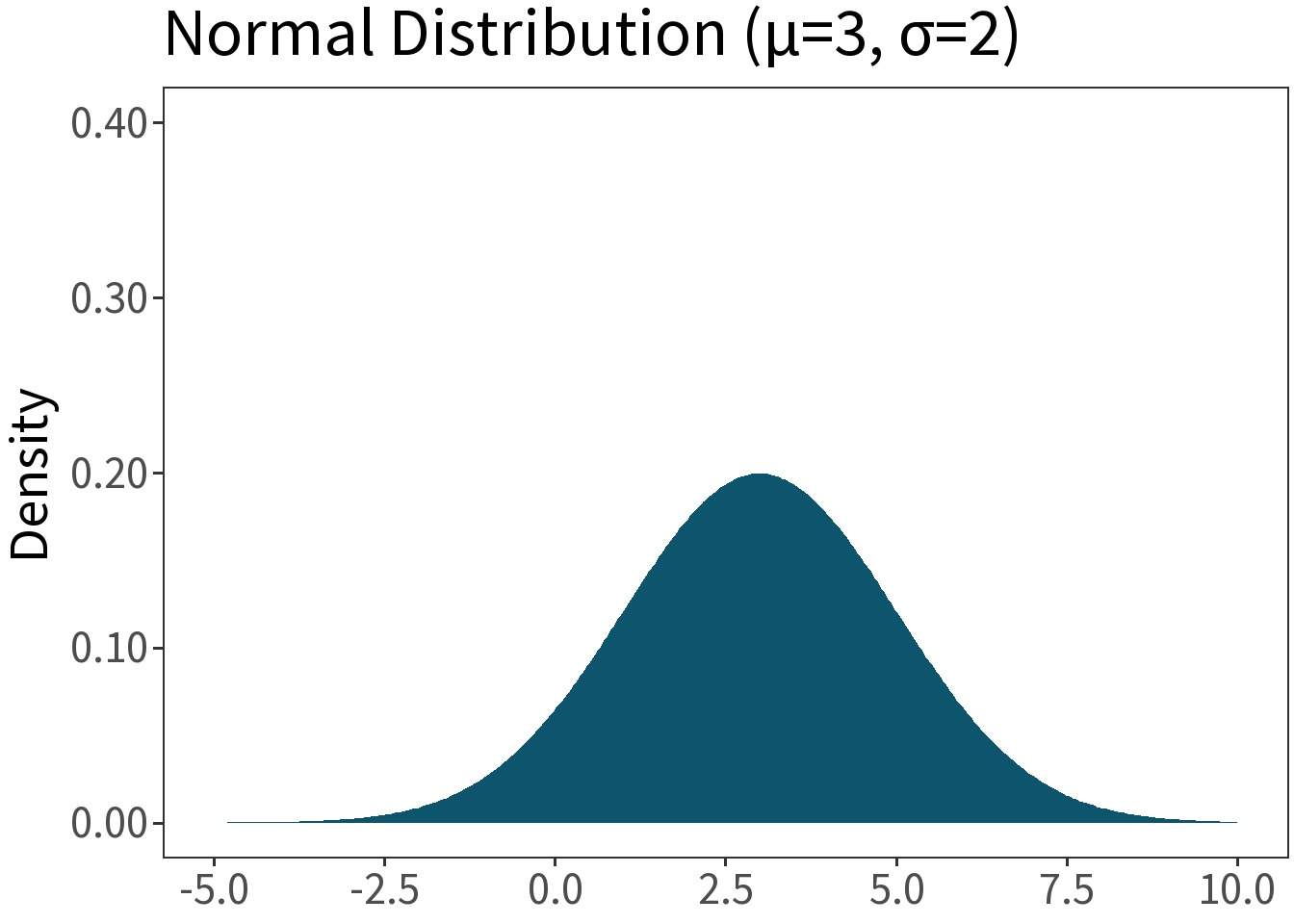
Bringing it all together
🚗 Cars Model
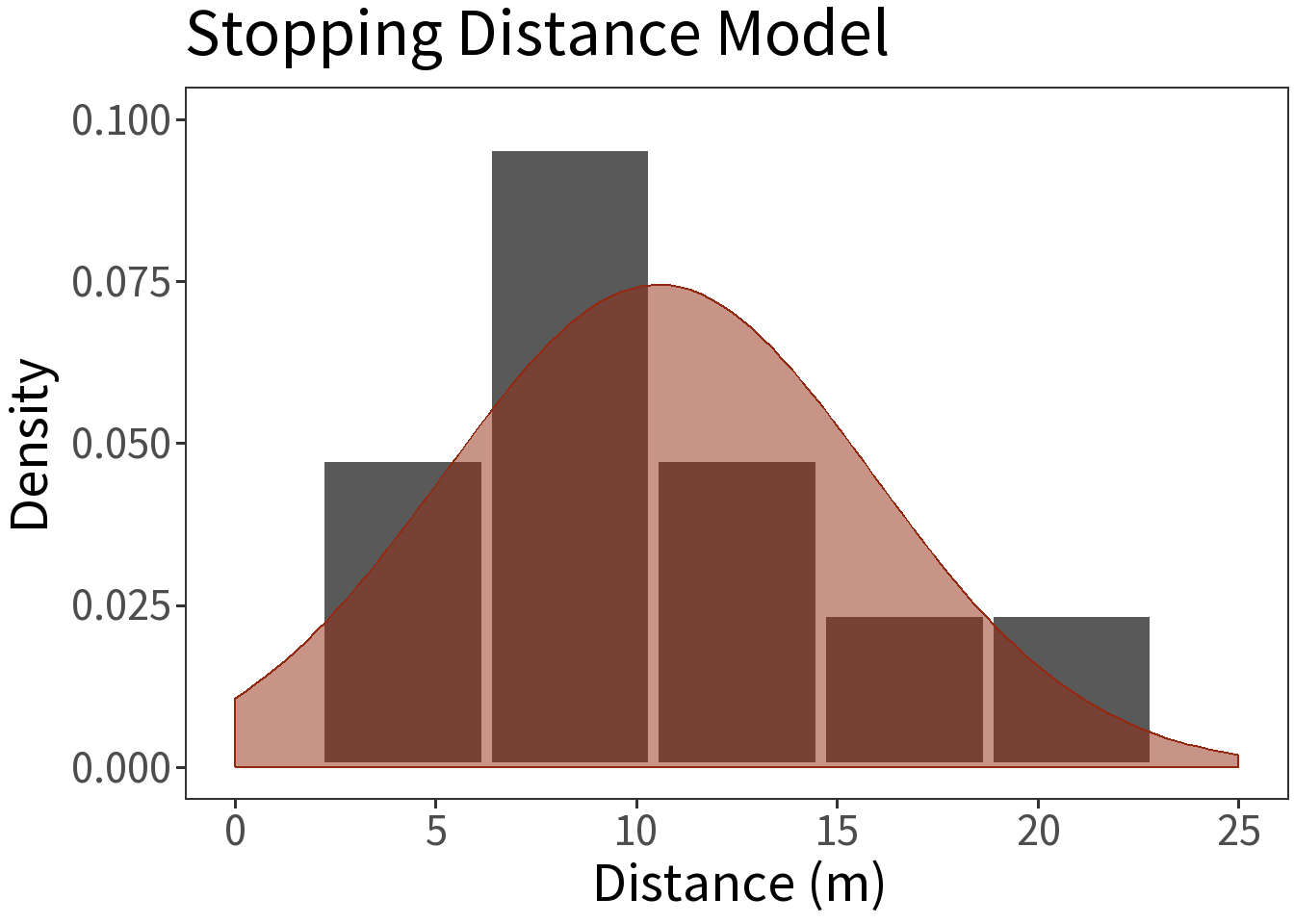
Let’s use the Normal distribution to describe the cars data.
- \(Y\) is stopping distance for population
- \(Y\) is normally distributed, \(Y \sim N(\mu, \sigma)\)
- Experiment is a random sample of size \(n\) from \(Y\) with \(y_1, y_2, ..., y_n\) observations.
- Sample statistics (\(\bar{y}, s\)) approximate population parameters (\(\mu, \sigma\)).
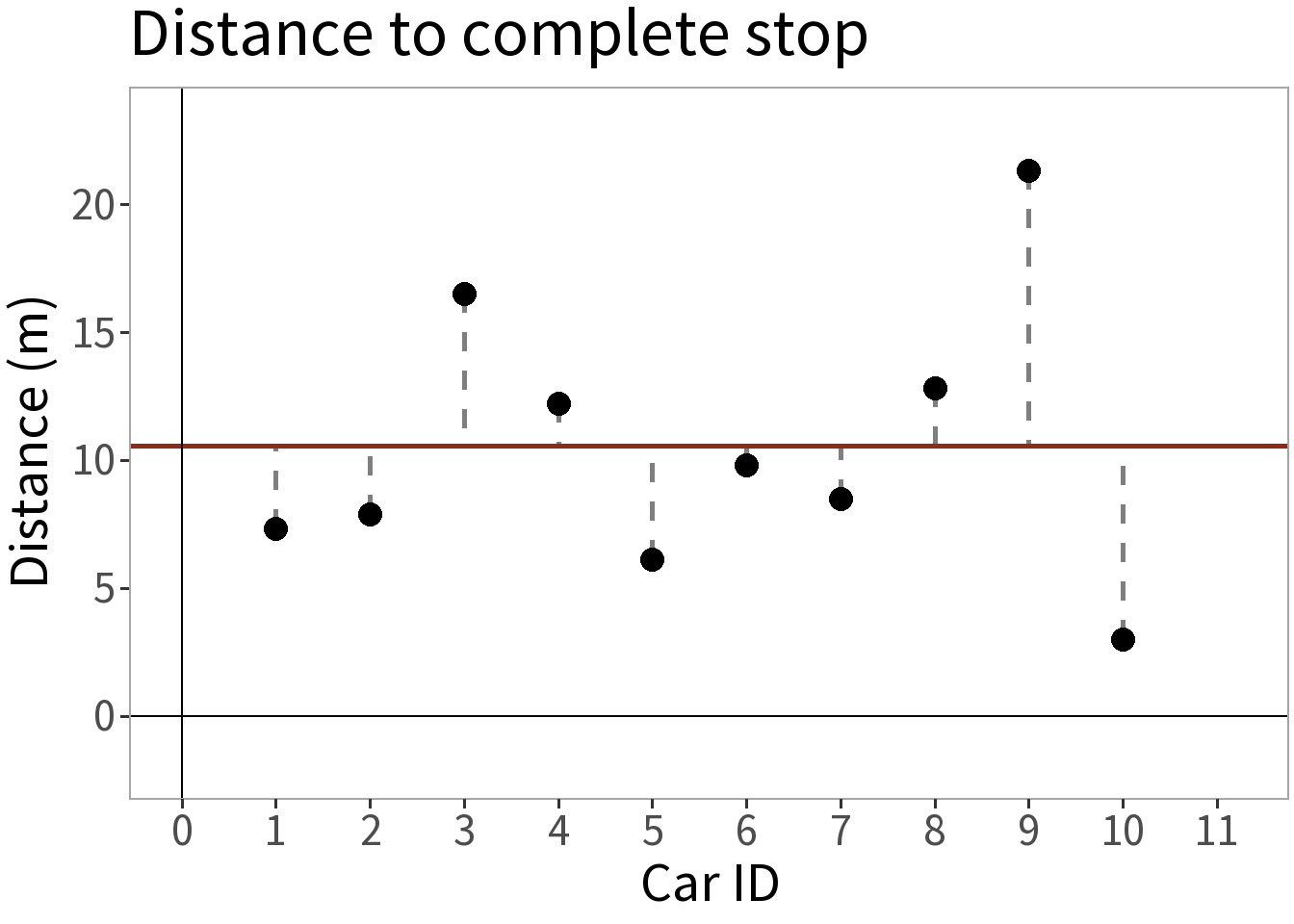
Sample statistics:
- Mean (\(\bar{y}\)) = 10.54 m
Sample statistics:
- Mean (\(\bar{y}\)) = 10.54 m
This is our approximate expectation
- \(E[Y] = \mu \approx \bar{y}\)
Sample statistics:
- Mean (\(\bar{y}\)) = 10.54 m
But, there’s error, \(\epsilon\), in this estimate.
- \(\epsilon_i = y_i - \bar{y}\)
Sample statistics:
- Mean (\(\bar{y}\)) = 10.54 m
The average squared error is the variance:
- \(s^2 = \frac{1}{n-1}\sum \epsilon_{i}^{2}\)
Sample statistics:
- Mean (\(\bar{y}\)) = 10.54 m
- S.D. (\(s\)) = 5.353 m
This is our uncertainty, how big we think any given error will be.
Sample statistics:
- Mean (\(\bar{y}\)) = 10.54 m
- S.D. (\(s\)) = 5.353 m
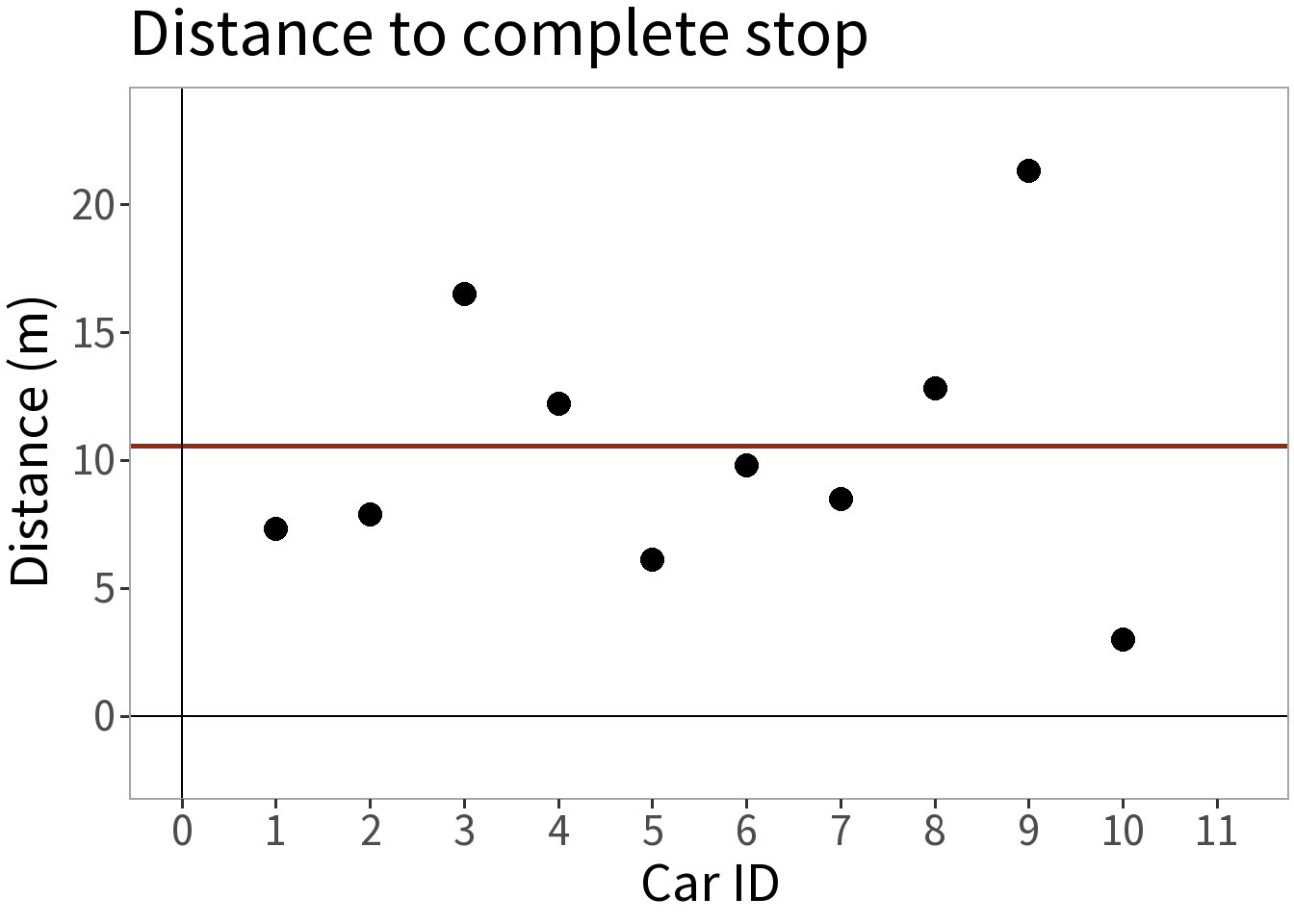
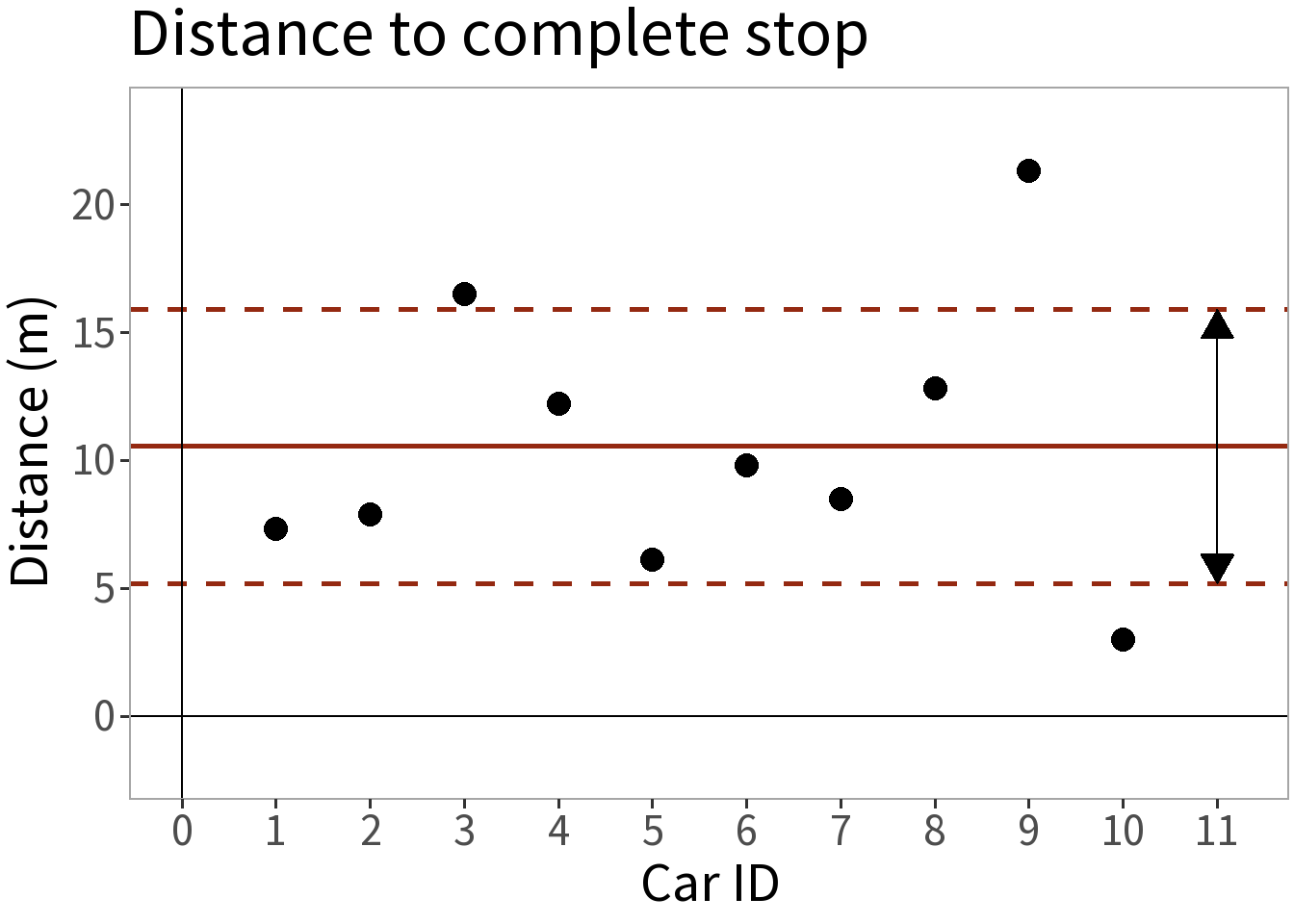
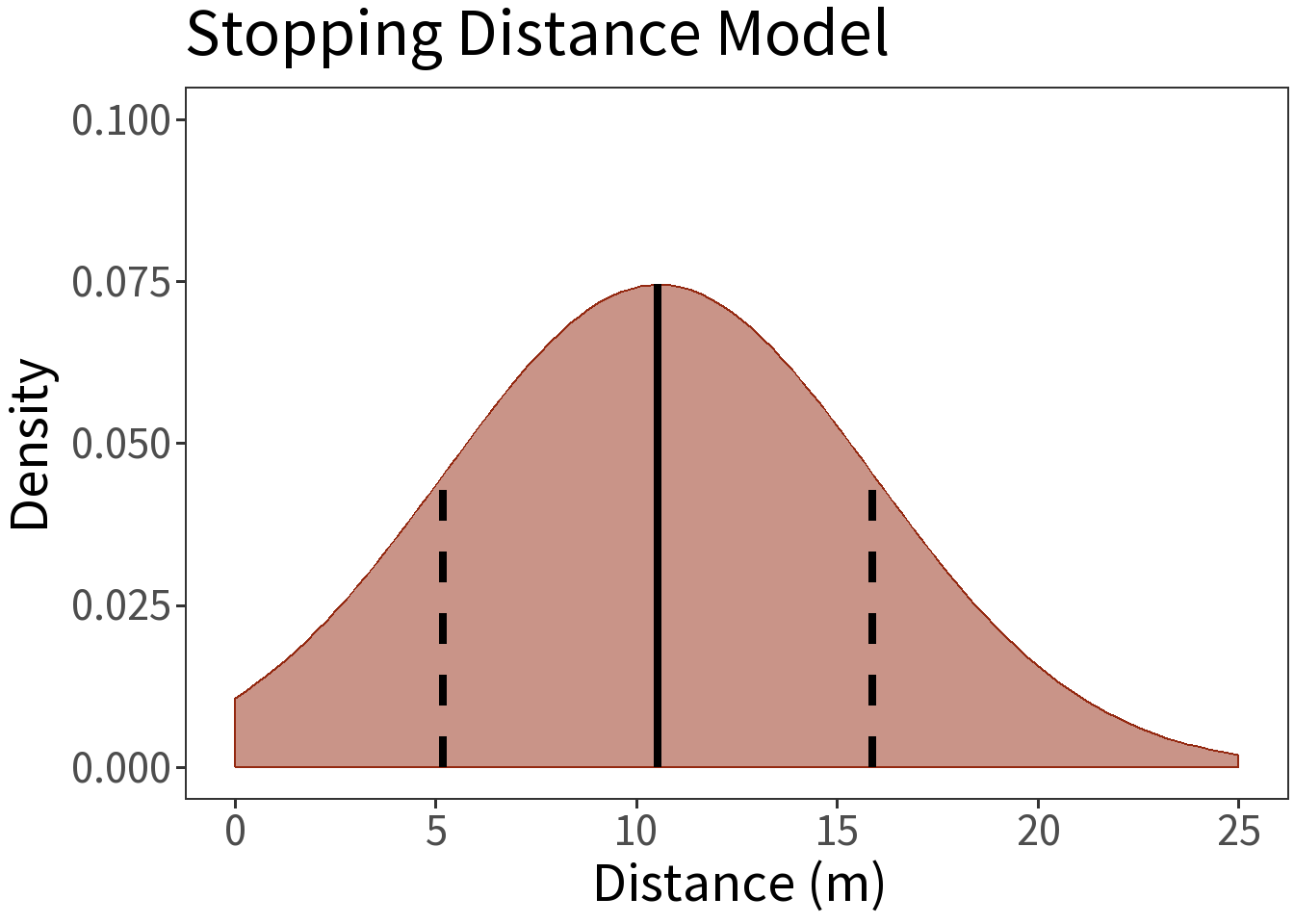
So, here is our probability model.
\[Y \sim N(\bar{y}, s)\] This is only an estimate of \(N(\mu, \sigma)\)!
Sample statistics:
- Mean (\(\bar{y}\)) = 10.54 m
- S.D. (\(s\)) = 5.353 m
With it, we can say, for example, that the probability that a random draw from this distribution falls within one standard deviation (dashed lines) of the mean (solid line) is 68.3%.
A Simple Formula
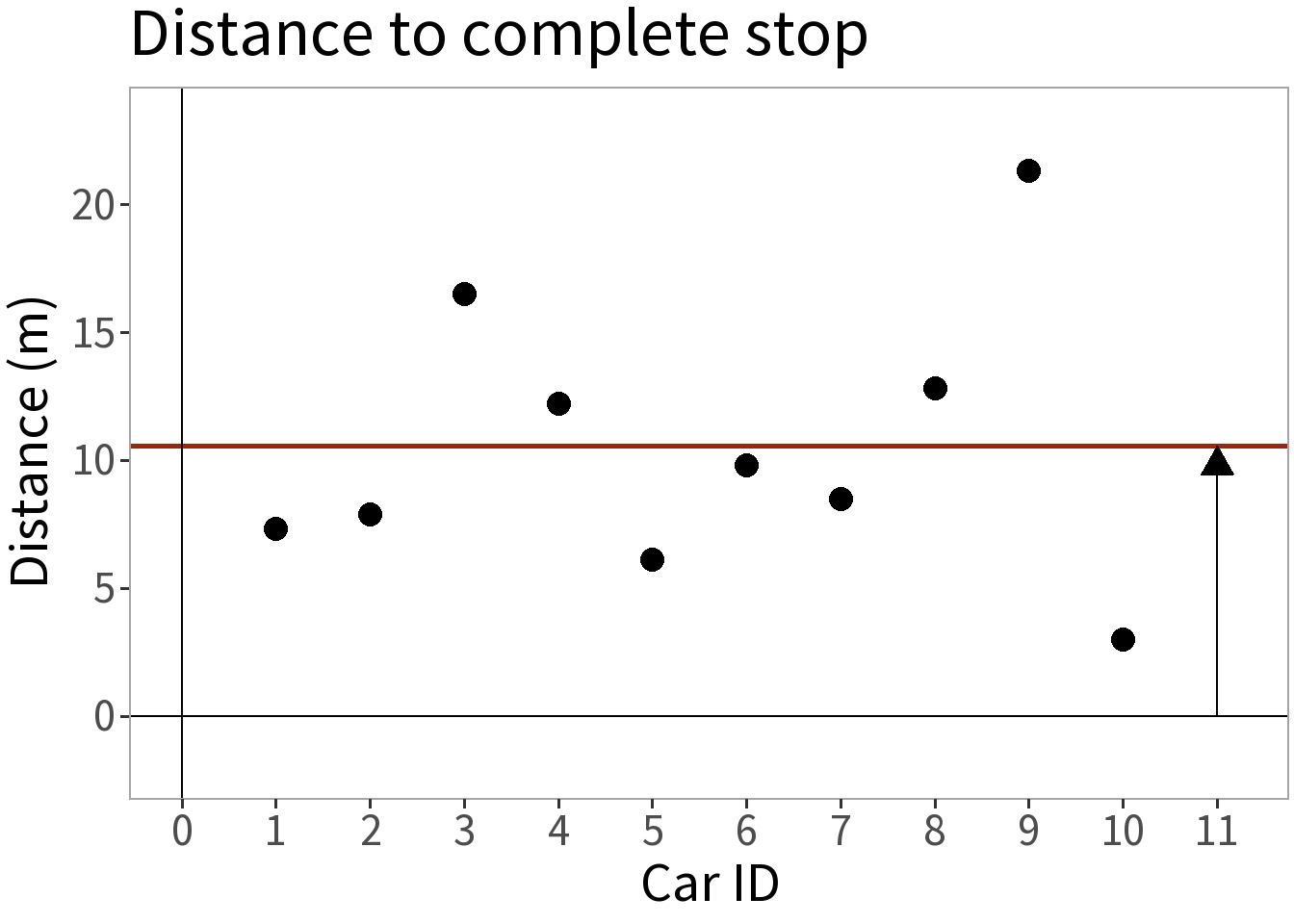
This gives us a simple formula
\[y_i = \bar{y} + \epsilon_i\] where
- \(y_i\): stopping distance for car \(i\), data
- \(\bar{y} \approx E[Y]\): expectation, predictable
- \(\epsilon_i\): error, unpredictable
This gives us a simple formula
\[y_i = \bar{y} + \epsilon_i\]
If we subtract the mean, we have a model of the errors centered on zero:
\[\epsilon_i = 0 + (y_i - \bar{y})\]
This gives us a simple formula
\[y_i = \bar{y} + \epsilon_i\]
If we subtract the mean, we have a model of the errors centered on zero:
\[\epsilon_i = 0 + (y_i - \bar{y})\]
This means we can construct a probability model of the errors centered on zero.
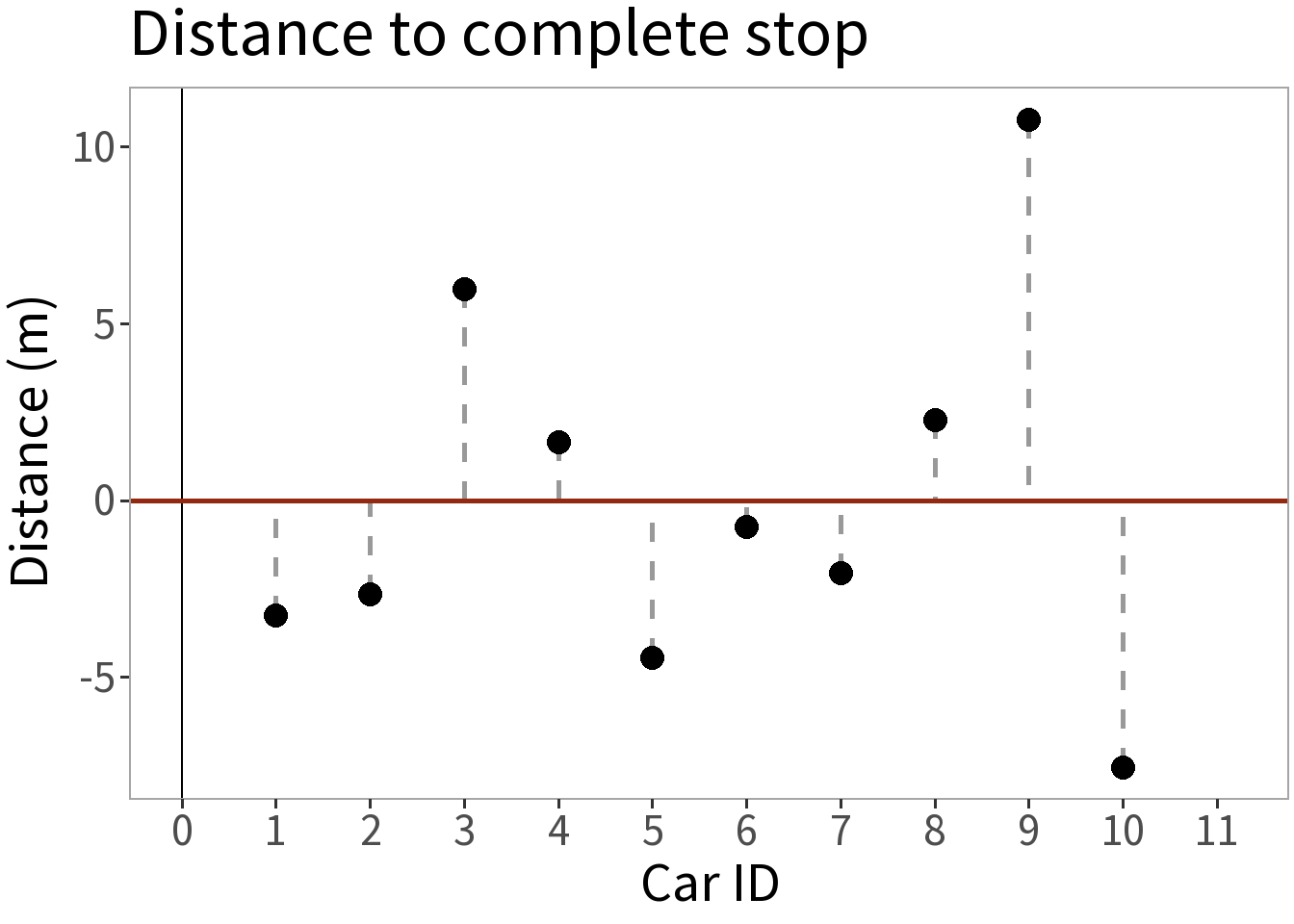
Probability Model of Errors
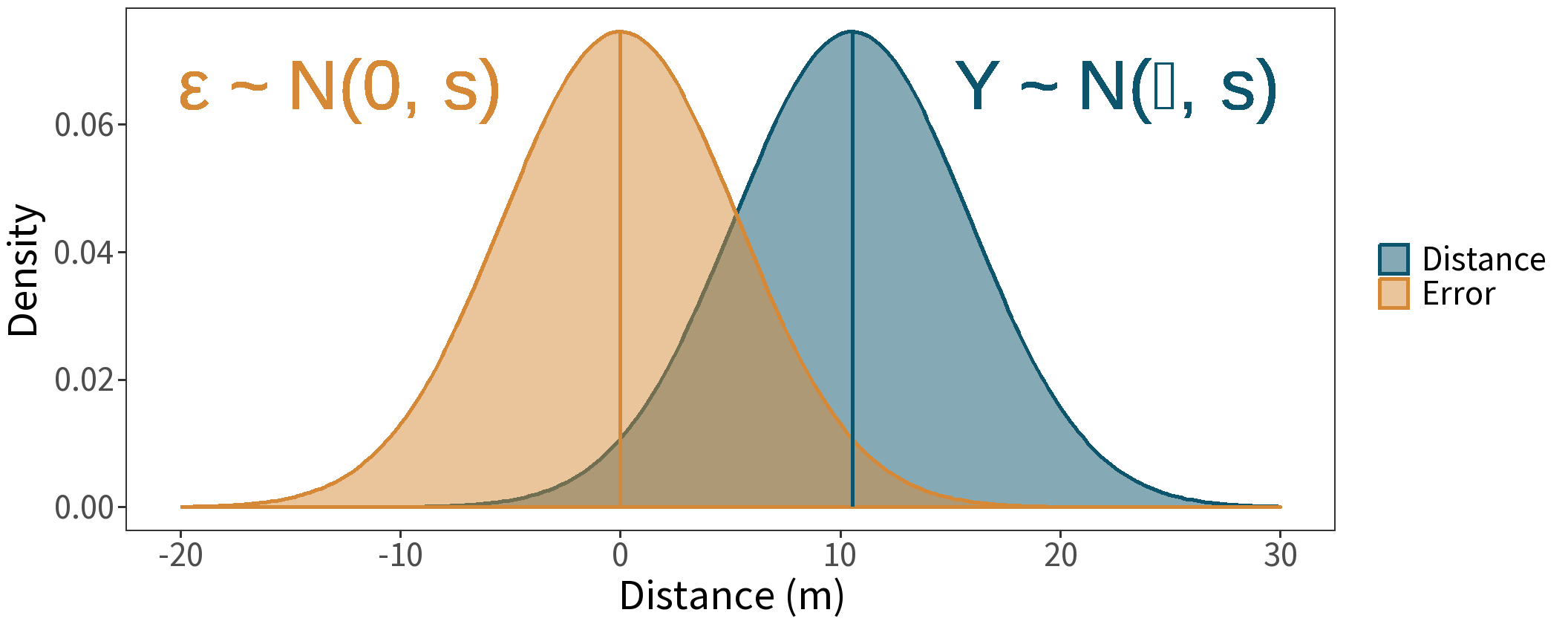
Note that the mean changes, but the variance stays the same.
Summary
Now our simple formula is this:
\[y_i = \bar{y} + \epsilon_i\] \[\epsilon \sim N(0, s) \]
- Again, \(\bar{y} \approx E[Y] = \mu\).
- For any future outcome:
- The expected value is deterministic
- The error is stochastic
- Must assume that the errors are iid!
- independent = they do not affect each other
- identically distributed = they are from the same probability distribution
- The distribution is now a model of the errors!